
Galilei elévülhetetlen érdeme, hogy megállapította, hogy az ingamozgás periódusa a testek súlyától, anyagi minőségétől független, csak az inga hosszától függ. A XVII. századig a legtöbb mechanikus óra ún. fólió-szabályozással működött. Az ábra szerinti óraszerkezet középpontjában helyezkedik el a fogazott koronakerék, amelynek tengelyére egy dob van rögzítve:
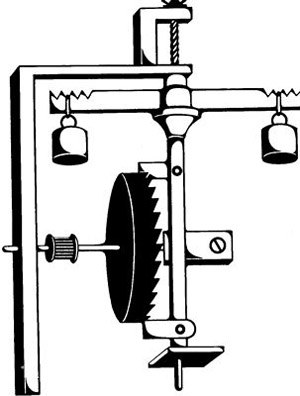
Fóliószabályozás. A dobra egy nem ábrázolt kötél van feltekerve a végén egy súllyal. (https://www.sztnh.gov.hu/hu/kiadv/ipsz/200506/06-technika-szilagyi.html)
A dobra egy nem ábrázolt kötél van feltekerve a végén egy súllyal. Ez a súly működteti az órát, elforgatva a koronakereket az óramutató járásával ellenkező irányba. A függőleges tengelyre két retesz van rögzítve, amelyek a koronakerék fogaihoz kapcsolódnak. A tengelyre egy vízszintes rúd, a fólió van rögzítve, amelyről súlyok függenek. A koronakerék fogaiban felütköző reteszek a kerék forgásával alternáló elfordulásra késztetik a fóliót, amely ide-oda billeg, miközben a koronakerék fokról fokra elfordul. Ez a fokonkénti legördülés adja az óra ritmusát, amely a mutatók egy-egy időegységnyi elmozdulásában jelenik meg. Az óra ritmusát a fólión lévő súlyok által kifejtett forgatónyomaték változtatásával lehetett szabályozni, azaz a súlyok kifelé vagy befelé történő elmozdításával. Ha az óra például sietett, akkor a fólió súlyait kifelé mozgatták, lassítva ezzel a ritmust. A fóliószabályozás pontossága igen korlátozott volt, napi 15 perc körül ingadozott.
Galilei a szabadesés törvényszerűségeinek vizsgálata közben jutott el az inga mozgástörvényeinek vizsgálatához, mivel feltételezései igazolásához ingára volt szüksége. Ő még csak hipotézisként feltételezte, hogy egy lejtőn eső test sebessége kizárólag a lejtő magasságától függ. A tételt egy inga segítségével demonstrálta. Az ingát meghatározott szöggel kitérítette, majd a súlyt tartó fonál útjába lengés közben egy akadályt helyezett úgy, hogy a súly kisebb sugáron lengett tovább. Azt találta, hogy a test ilyenkor ugyanolyan magasságig emelkedik, mint amilyen magasságból eredetileg indította a testet. Ebben a meglátásban csírájában már az energiamegmaradás elvét, pontosabban a kinetikus és potenciális energia egymásba alakulását lehet felfedezni.
Idézzünk tovább a Viviani-féle levélből: "...Galilei látása annyira megromlott, hogy a tervet megrajzolni és a modellt elkészíteni nem tudta, azért elképzelését elmondta saját fiának. Galilei 1642-ben január 8-án meghalt. Fia az órát egy fiatal lakatossal elkészíttette, munka közben az alkatrészeket, súlyokat, ingát nekem megmutatta."

Galilei tervei alapján 1883-ban készített modell
(https://www.sztnh.gov.hu/hu/kiadv/ipsz/200506/06-technika-szilagyi.html)
Az ingaóra feltalálásáról egy másik történet is szól, mely szerint Rómában élt a két Campani testvér, távcsöveket, mikroszkópokat, órákat készítettek. Érdekes éjszakai órájuk ma is megvan, belülről fényforrás világítja meg a számokat. Óráik fólió- és kerékgátlásúak voltak. Egy napon Farnese bíboros olyan órát rendelt a műhelyben, ami ketyegő hangjával az alvót nem zavarja. A Campanik megígérték, hogy mindent megpróbálnak. Egy folióbillegős asztaliórát elfordítottak úgy, hogy a fólió függőleges síkban lengjen. A lassúbb járás érdekében a foliórúd végeire pótsúlyt erősítettek. Próba közben az egyik nehezék levált, és az óra - legnagyobb megrökönyödésükre - tovább járt, az alul lévő kar ugyanis mint inga lengett tovább.
Leonardo da Vinci is tanulmányozta az inga alkalmazásának lehetőségét, ő nemcsak szabályozóelemként, hanem hajtóműként is alkalmazni kívánta. Leonardo sokat foglalkozott az órákkal, számos rajza tanúskodik erről. Galilei előtt már az ingás gátszerkezet tervét is lerajzolta, és ébresztőórát is tervezett. Az ébresztőóra úgy működött, hogy az alvó lábát a megfelelő időben megrántotta. A Madridi kódex I. kötetében teljes óraterve is látható. Egyik rajzán a motor áttételek útján négyszárnyú szélkereket forgat, ezzel a légellenállást hasznosítva gátlóművében.
Az első ingaóra 1656 decemberében készült, és sokkal pontosabb volt bármely korábbi óránál. Ez az óra körülbelül három óra alatt tévedett egy másodpercet, míg a fólió-szabályozású órák néhány perc alatt késtek vagy siettek ennyit.
Bár Galilei, amikor az inga használatát felismerte, és egy új fajta gátszerkezetet képzelt el, de Huygens súllyal működtetett hagyományos orsós szabályozást használt. Az orsójárat oszcilláló tagja nagy szögben mozog, és Huygens felismerte, hogy ha egy inga ilyen nagy kilengést végezne, a lengés állandósága nem lenne fenntartható. Ennek elkerülésére fogaskerék-áttételt alkalmazott, hogy az orsó nagyobb szögben forogjon, mint az inga lengése. Az inga lengésideje a súly lefelé vagy felfelé mozdításával szabályozható. Így válik érthetővé, hogy bár Galilei volt a "nagy ingás", az ingaóra mégis Huygens nevéhez köthető.
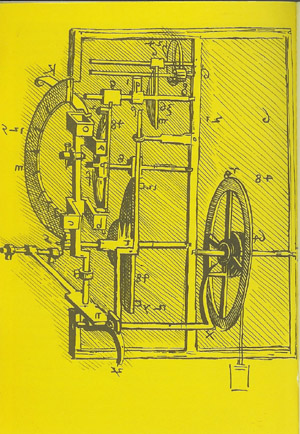
Galilei óraterve (https://www.sztnh.gov.hu/hu/kiadv/ipsz/200506/06-technika-szilagyi.html)
Sokkal megbízhatóbb órákat tett lehetővé az inga lengésére alapozott szabályozás, hiszen az inga lengésideje állandó. Galilei 1582-ben a pisai katedrálisban megfigyelte egy kötélen függő lámpa ingását, és úgy találta, hogy az ingamozgás periódusa a közben eltelt hosszú idő alatt is alig változott. 1637-ben született az az ötlete, hogy az óra vezérlését is lengő súllyal kellene megoldani úgy, hogy a súly egy-egy lengésére egy kerék fordulna el egy bizonyos szögmennyiségnyit. Ekkorra Galilei már megvakult, így elgondolását fiával és a tanítványával fejlesztette ki, akik megrajzolták elképzelését. Fia elkezdte megépíteni az órát, amelynek aztán az évszázadok során nyoma veszett. Galilei 1642-ben meghalt, fia pedig 1649-ben, az óráról fennmaradt egyetlen vázlatot tanítványa rajzolta 1659-ben. A Galilei által tervezett óra még nem volt működőképes, azonban így is nagyon fontos állomás, mivel ez volt az első kísérlet az inga alkalmazására az óra szabályozásában.

Galilei sírja (1642, https://hu.wikipedia.org/wiki/Galileo_Galilei)
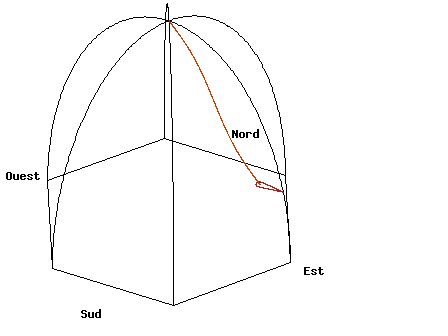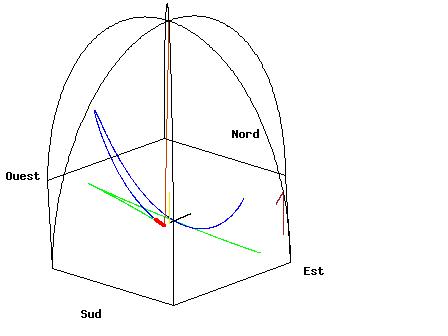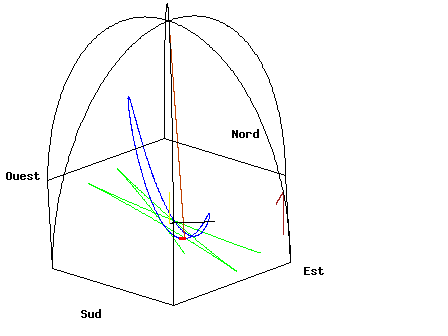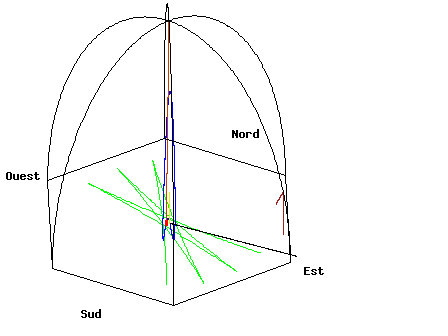
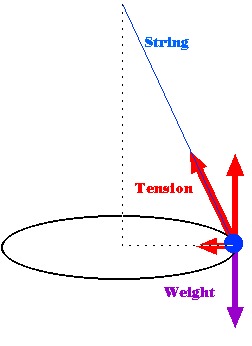
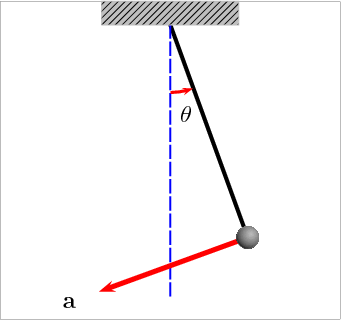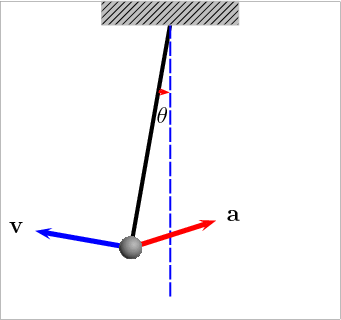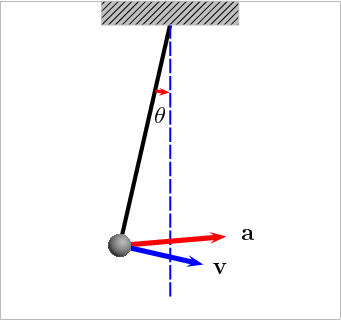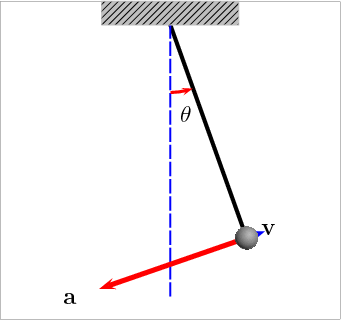
A Foucault-inga (https://hu.wikipedia.org/wiki/Foucault-inga) a Föld forgásának és a Coriolis-erő hatásának szemléltetésére szolgáló kísérleti eszköz. Az ingának azon a tulajdonságán alapul a működése, hogy egy inga megtartja a a lengési síkját, amíg külső erő nem hat rá. Ha hosszú a felfüggesztése, az inga hossza, akkor olyan sokáig leng, hogy a Föld elforog alatta.



Eötvös műszerei, a görbületi variométer és a horizontális variométer, 1890-ben a Magyar Optikai Művek elődjében, Süss Nándor finommechanikai műhelyében készültek. Az 1900-as párizsi világkiállításon bemutatott és díjat nyert egyszerű nehézségi variométer 1898-ban készült. Az első, nagyobb területre kiterjedő módszertani gravitációs mérést 1901-ben és 1903-ban a befagyott Balaton jegén a Balaton bizottság lelkes vezetője, id. Lóczy Lajos támogatásával végezték. A sima Balaton-felszín nagyon alkalmas volt a mérések szempontjából, mert nem kellett figyelembe venni a terepfelszín egyenetlenségeiből adódó hatást. Ezeket számos további terepi mérés követte, amelyekkel az inga földtani kutatásban való hasznosíthatóságát vizsgálták. Végül a földmérők 1912-ben Hamburgban rendezett XVII. konferenciáján Eötvös elérkezettnek látta az időt, hogy a gyakorlati alkalmazás elveit megfogalmazza. Az első sikeres olajkutatási célú gyakorlati méréseket Egbell környékén, a Morva-mezőn 1915-ben végezték – ezzel vette kezdetét a nyersanyagkutató geofizika, amelynek két évtizeden át uralkodó műszere Eötvös Loránd torziós ingája volt; alkalmazták többek között a texasi, a venezuelai és a közel-keleti olajterületek feltárásánál.

Johannes Kepler elsőként írta le az optikai lencsék tulajdonságait és használatát a könyveiben. Kepler újfajta, két domború lencsét tartalmazó (Kepler-féle vagy csillagászati) távcsövet épített, amely fordított állású képet adott ugyan, de csillagászati célokra alkalmasabb volt elődeinél. Az első tükrös távcsövet (reflektort) 1672-ben építette Isaac Newton, miután a fénytörés jelenségét vizsgálva ráébredt arra, hogy nemcsak a prizmák, hanem a lencsék is színeire bontják a fehér fényt, azaz a csillagok fehér pontok helyett színes foltok lesznek. A színhiba kiküszöbölhető, ha az objektív helyett homorú tükröt használunk. Jelenleg szinte minden komoly, nagy teljesítményű távcső reflektor, mivel a tükröket olcsóbb és egyszerűbb előállítani, továbbá egy méternél nagyobb átmérőjű lencséket gyakorlatilag lehetetlen a szükséges pontossággal előállítani, és torzulás mentesen távcsőtubusba szerelni. Napjainkban több, 10 méter körüli tükörátmérőjű csillagászati távcső működik, és megkezdődött egy 24,5 méteres is. A Newton-féle távcső mára több változatban létezik, de a reflektorok népszerűsége töretlen; a Hubble űrtávcső is tükrös rendszerű. A kisebb távcsövek—műszerek, kamerák, binokulárok — mind lencsések.
