LAPULTSÁG → CSÚCSOSSÁG DEF.

 
 
 
 
LAPULTSÁG  → CSÚCSOSSÁG DEFINÍCIÓ
(KURTOSIS → DEFINITION OF PEAKEDNESS*) 
 
(2022 december)
 
 
 

A valószínűségelméletben és a statisztikában a lapultság (https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis, görögül: κυρτός, kyrtos jelentése "görbe, íves") egy valós értékű véletlen változó valószínűségi eloszlásának a "szélességét", a várható értékétől távoli adatok gyakoriságát leíró mérték. A távoli adatok súlyát, és nem az adatok átlaghoz közeli konfigurációját írja le. Leggyakrabban relatív negyedik momentumot használják: κ = μ4/σ4 - t.: a lapultság a standardizált adatok negyedik hatványának várható értéke, normális eloszlás esetén 3. 

 Moors szerint standardizált z változókra: ha z = (X -  μ)/σ, ahol  X egy véletlen változó, μ a várható értéke, és σ a szórása, és a lapultság  κ = E [ z4] , ahol E várható értéket jelöl, és mert standardizált változókra σ4 = 1, ekkor  κ =  E[ z4]  = var [ z2] + [ E[ z2] ]2 = var [ z2] + 1. A normális eloszlástól való eltérést is használják, ekkor 3 -mal csökkentik az értékét. Következik, hogy  κ = var [ z2]  + 1 reciproka kapcsolatos a csúcsossággal.

Definíció: 1/κ = csúcsosság.  

Ha  k > 0, akkor a z standardizált változó esetén a Cantelli (https://en.wikipedia.org/wiki/Cantelli%27s_inequality)  egyenlőtlenség 

 
alakú.
 
 
Amikor  k2 =  var [ z2] = E [ z2 - E (z2)] 2 = D 2 (z2),  akkor a Cantelli egyenlőtlenség:
 
                                                                                                                           P { z  ≥ D [ z2] }  ≤ 1/κ.
 
(Mert: Moors szerint  κ = k2 + 1 = E[ z4] = var [ z2] + [ E[ z2] ]2 = var [ z2] + 1, ahol κ a lapultság mértéke, Moors, J. J. A. (1986), "The meaning of kurtosis: Darlington reexamined", The American Statistician, 40 (4): 283–284), https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis). 
 
1/ κ  értékek:  normális eloszlás esetén 1/3, egyenletes eloszlás esetén 5/9, és exponenciális eloszlás esetén 5/6, Laplace eloszlás esetén (https://en.wikipedia.org/wiki/Laplace_distribution) 1/6, továbbá Bernoulli eloszlás esetén: (1 - p) / [1- 3p(1-p)], és (1 - p)/ (p2 - 9p + 9)  geometriai eloszlás (https://testbook.com/question-answer/the-excess-kurtosis-of-the-geometric-distribution--607e64a9c3ce62d9a72ef003) esetén (1 - p)/[6 + p2/(1-p)] értékű, logisztikus eloszlás esetén 0.238, Wigner eloszlás esetén 0.5 értékű, Poisson eloszlás esetén  λ.
 
 
Lapultság κ -3  értékek és sűrűségfüggvények eloszlásokhoz 0 várható értékkel, 1 varianciával:
A lapultság 3-al csökkentett értékét használják, a normális eloszlásé ekkor 0  lapultságú.
D: Laplace-eloszlás, más néven kettős exponenciális eloszlás, lapultság többlet a normális eloszláshoz viszonyítva = 3
S: hiperbolikus szekáns eloszlás, narancssárga görbe, lapultság többlet a normális eloszláshoz viszonyítva = 2
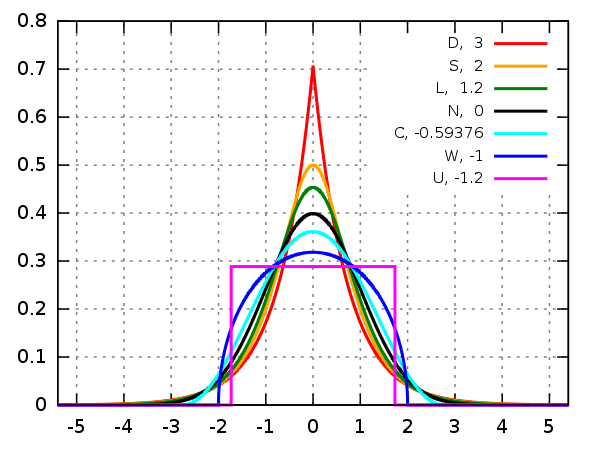
L: logisztikus eloszlás, zöld görbe, lapultság többlet a normális eloszláshoz viszonyítva = 1,2
N: normális eloszlás, fekete görbe (fordított parabola a logaritmikus diagramon), lapultság többlet a normális eloszláshoz viszonyítva = 0
C: emelt koszinusz eloszlás, ciánkék görbe, lapultság többlet a normális eloszláshoz viszonyítva = -0,593762...
W: Wigner-félkör eloszlás, kék görbe, lapultság többlet a normális eloszláshoz viszonyítva = -1
U: egyenletes eloszlás, magenta görbe (az egyértelműség kedvéért mindkét képen téglalapként látható), lapultság többlet a normális eloszláshoz viszonyítva = -1,2.
600px Standard symmetric pdfs.svg
 
Sűrűségfüggvények 0 várható értékkel és egységnyi szórással, és  κ - 3, azaz a lapultság hárommal csökkentett értékei
 
 
* Please, see below 
*********************************************************************************************************************************************************************************************************************************************************************
 
*KURTOSIS → DEFINITION OF PEAKEDNESS 
 
(December 2022) 
 
 
 
 
In probability theory and statistics, flatness (https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis, Greek: κυρτός, kyrtos meaning "curve") is a measure of the "width" of the probability distribution of a real-valued random variable, describing the frequency of data far from the expected value. Flatness describes the weight of the distant data, not the configuration of the data close to the mean. Most often used as a relative fourth moment of κ = μ4/σ4 - t.: flatness is the expected value of the fourth power of the standardised data, which is 3 for a normal distribution.
 
For standardised variables z according to Moors: if z = (x - μ)/σ, where x is a random variable, μ is its expected value and σ is its standard deviation, then flatness κ = E[z4] , E denotes expected value, and because for standardised variables σ 4 = 1, then κ = var [ z 2] + [ E[z 2] ] 2 = var [ z 2] + 1.
It follows that the reciprocal of var [z 2] + 1 is related to the kurtosis.
 
If k > 0, then for the standardized variable z, the Cantelli (https://en.wikipedia.org/wiki/Cantelli%27s_inequality)
inequality
 

holds, and when  k2 = var [ z 2]  :

                                                                 P { z ≥ var [ z 2]  1/2 } ≤ 1/κ, where κ = kurtosis,


1/κ = σ4/  μ4, and for k 2 + 1 = κ = E[ z 4] = var [ z 2] + [ E ( z 2) ] 2 = var [ z2] + 1 by Moors. (Moors, J. J. A. (1986), "The meaning of kurtosis: Darlington reexamined", The American Statistician, 40 (4): 283-284) and https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis) and where var [ z2] = E [ z2 - E(z2)]2 .
 
 

 Values of κ - 3 are defined as excess kurtosis:

 
Probability density functions for selected distributions with mean 0, variance 1 and different excess kurtosis (https://en.wikipedia.org/wiki/Kurtosis)