A kvantumszámítógépekről egyszerűen
(2025 október)
A kvantumszámítógép egy újfajta számítógép, amely hatékony az összetett problémák megoldásában, de közel -273 fokon működik. A biteket (0-kat vagy 1-eket) használó klasszikus számítógépekkel ellentétben a kvantumszámítógépek „qubiteket” használnak, amelyek bár lehetnek 0 és 1 állapotban is, de egy szuperpozíciónak nevezett tulajdonság miatt, egy időben mind a két állapotban is lehetnek, ami lehetővé teszi, hogy képesek valós időben megoldani olyan problémákat, amelyek a szuperszámítógépeknek sok év kell.
A Q-gépek működése: a hagyományos számítógép egyszerre egy lehetőséget számol végig, addig egy kvantumszámítógép egyszerre képes sok, vagy az összes lehetőséget végigszámolni. A kvantumszámítógépek qubitek-et használnak, amelyek egyszerre 0 és 1 „szuperpozícióban” ia lehetnek. A qubitek összekapcsolhatóak egy kvantumösszefonódás-nak nevezett jelenség következtében, állapotaik összefüggenek, függetlenül attól, hogy milyen messze vannak egymástól,(amin nincs mit érteni, valójában nem is értjük), ami egy különös tulajdonság. A kvantumtulajdonságok következtében a kvantumszámítógépek gyorsabban tudnak kezelni összetett számításokat, pl. a véges hosszúságú jelszavak feltörését. Van védekezés a feltörés ellen, ha csak kis számú próbálkozást engedélyezünk. A kvantumszámítógépek nem a laptopok helyettesítésére szolgálnak, hanem speciális problémák megoldására tervezik a Q-gépeket. Pl.: a gyógyszerkutatás és az anyagtudományi szimuláció, a pénzügyi modellezés, és a modern titkosítási kódok feltörésére, szorzatok tényezőkre való bontására. A Q-gép nem általános célú számítógép, soha nem lesznek hasznosak mindennapi feladatokhoz (-273 C fokon működnek), például webböngészéshez vagy szövegszerkesztéshez.

A kvantumszámítógép (1981-ben Richard Feynman Nobel-díjas fizikus találta ki a kvantumszámítógép kifejezést) gyakorlati megvalósítása a kezdeti lépéseknél tart, kísérleti fázisban van. A kvantummechanikai hatások miatt a rendszert közel abszolút nulla fokra kell folyamatosan hűteni, a vezetékei is hűtött koaxiális kábelek, melyek szupravezető tulajdonságúak, a vezetékek is alacsony hőmérsékleten működnek. A bemenetet mikrohullámú impulzusok jelentik, melyek beállítják a részecskék állapotait. (https://hu.wikipedia.org/wiki/Kvantumsz%C3%A1m%C3%ADt%C3%B3g%C3%A9p) 2024-ben a Google bejelentette, hogy a Willow kvantumchipet használó kvantumszámítógépe olyan feladatot oldott meg percek alatt, amely a világ akkori legerősebb szuperszámítógépének több milliárd évig tartott volna.
A qubit (esetenként qbit) a kvantum-információelméletben az információ alapegysége, a kvantumszámítógépekben a bit megfelelője, melyeket a Q-gép logikai kapukkal dolgoz fel. A klasszikus bit egyértelműen vagy a  , vagy az
, vagy az  állapotot jelöli, addig egy qubit lehet a két állapot szuperpozíciójában is, ekkor az állapotát a következőképp adjuk meg: legyenek
állapotot jelöli, addig egy qubit lehet a két állapot szuperpozíciójában is, ekkor az állapotát a következőképp adjuk meg: legyenek  és
és  komlex számok, melyekre
komlex számok, melyekre  . A feltétel* következménye, hogy az eredmény
. A feltétel* következménye, hogy az eredmény  valószínűséggel
valószínűséggel  ,
,  valószínűséggel pedig
valószínűséggel pedig  lesz. Az
lesz. Az  érték pedig pl. azt az esetet írja le, amikor a qubit a két állapot egyenlő szuperpozícióban van, és kiolvasásakor 50% eséllyel lesz
érték pedig pl. azt az esetet írja le, amikor a qubit a két állapot egyenlő szuperpozícióban van, és kiolvasásakor 50% eséllyel lesz  , és 50% eséllyel lesz
, és 50% eséllyel lesz  az eredmény. Általában
az eredmény. Általában  és
és  négyzetösszege a [0,1] zárt intervallumba esik.
négyzetösszege a [0,1] zárt intervallumba esik.
A kvantumbit nullát, egyet vagy ezek kvantum-szuperpozícióját tartalmazhatja, ami végtelen számú állapotot tesz lehetővé. A kvantumszámítógépekben a kvantumbitek egy lehetséges megvalósítása két féle spinállapotú részecskékkel történik, valójában azonban bármely megfigyelhető mennyiség megfelelő jelölt lehet kvantumbitek megvalósítására, amelyik az idő múlásával megmarad, és amelynek van legalább két, diszkrét és jól megkülönböztethető sajátértéke. A kvantumszámítógép a számításokat egymással párhuzamosan hajtja végre, ezért programozásához sajátos programozási módszer, átlagolás szükséges.
Egy kvantumszámítógépben a kvantumbiteket a klasszikusan megengedett állapotok szuperpozíciójával adhatjuk meg., a regisztert egy Q-hullámfüggvény írja le. (A kvantumállapotokat hullámfüggvények, állapotvektorok írják le, amelyek valószínűségi amplitúdókat kódolnak.) Az algoritmus futása után után a regiszterben tárolt sok digites komplex vektort méréssel olvassuk ki a kvantumbit regiszterből. A kvantummechanika törvényei szerint a mérésnek az eredménye sok digites véletlen sorozat lesz, és a tárolt állapot megsemmisül. Mérnöki szemmel nézve egy olyan rendszert kell létrehozni, amelyik el van szigetelve mindentől, kivéve a kimenetet mérő és a vezérlő mechanizmusokat. Továbbá ki kell kapcsolnunk a kvantumbitek és a mérés közötti csatolást, hogy ne oltsuk ki a kvantumbiteket, miközben műveleteket végzünk velük. A kiolvasott véletlen bit sorozatokat használjuk a függvényérték kiszámítására, mivel (az alapelvből következően) a mért kimenő bit sorozat valószínűségi eloszlásának értékei a függvény helyes értéke körül sűrűsödnek. Az algoritmus ismételt futtatásával és a kimenet ismételt mérésével meghatározhatjuk a nagy valószínűséggel helyes eredményt. Tehát a kvantumszámítások valószínűségi jellegűek, átlagolással kapjuk a végeredményt. Adott problémáknál sok számítás ellenére a szükséges megoldási idő n négyzetgyökével arányos, míg a klasszikus számítógépnek (n + 1)/2 próbálkozás szükséges a válasz megtalálásához, ami nagyságrendi különbség, és az egyes problémák megoldásának idejét évekről másodpercekre csökkentheti.
A Q-számítástechnikában és a Q-mérésben a végeredményeket számos ismételt futtatás és mérés átlagolásával kapjuk, a kvantumkísérletet sokszor futtatjuk le, gyakran ezerszer, vagy milliószor. Minden futtatás bináris, diszkrét eredményt ad, 0 vagy 1 -et egy qubit esetében, majd átlagoljuk az eredményeket a kvantumállapot valószínűségi eloszlásának becsléséhez. Átlagolással becsüljük a mérés előtti kvantumállapotot. A Q-szimulációkban és fizikában (pl. kvantumos Monte Carlo módszer) valószínűségi mintavételezést alkalmazunk a fizikai mennyiségek becslésére, és a sok mintán átlagolunk, hogy kiszámítsuk a megfigyelhető mennyiségeket, például az energiát, a mágnesezettséget, vagy a korrelációs függvényeket. Egyes esetekben (mint például a kvantumösszefonódás vagy a hibajavítás) egyszeri mérésekre és a klasszikus utófeldolgozásra támaszkodunk, de még ekkor is az elmélet valószínűségi viselkedést feltételez, és statisztikai elemzéssel hitelesítjük az eredményt.
*
A kvantumfizika az exponensben van:

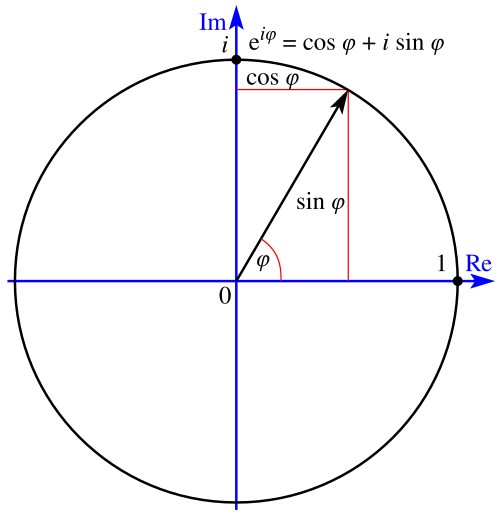




 komlex számok,
komlex számok,  . A feltétel* következménye, hogy
. A feltétel* következménye, hogy 




