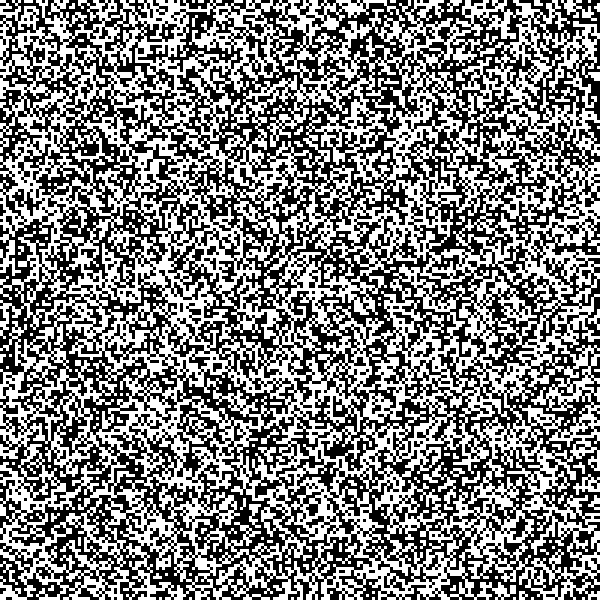ABSTRACT
A kaotikus rendszerek definíció szerűen megjósolhatlan viselkedésű, memórianélküli rendszerek. A már ismert kaotikus rendszerek determinisztikus, labilis rendszerek, a viselkedésük kezdőérték függő, és véges idő elteltével viselkedésük kaotikussá, megjósolhatatlanná válik. A kaotikus, vagy a kaotikussá váló viselkedés a kaotikus rendszerek belső (immanens) tulajdonsága, és a kaotikus viselkedés csak valószínűségi, sztochasztikus eszközökkel írható le. Az új kaotikus rendszerek, pl. várakozási időkkel, véletlen bolyongási problémákkal, véletlen számokkal, véletlen gráfokkal kapcsolatosak, a leírásuk az örökifjúság, a megjósolhatatlan viselkedés fogalmakkal, független növekményű, additív folyamatokkal történik. A memórianélküli rendszereknél az örökifjú folyamat jövője független a folyamat jelenétől és múltjától, melyek exponenciális vagy geometriai eloszlásúak. A független növekményű sztochasztikus folyamatokat memórianélküli, megjósolhatlan folyamatoknak nevezzük. A kaotikus rendszerek gyakran élettartamok, várakozási idők, általában valamilyen esemény bekövetkezéséig eltelt véletlen időtartamok hosszával kapcsolatosak.
A normális eloszlásnál a várható érték és a szórásnégyzet független mennyiségek, az egyenletes eloszlásnál a zérus várható érték és a szórásnégyzet, a terjedelem négyzete függetlenek. A Kálmán-szűrőben zérus várható értékű fehér Gauss-folyamatot, vagy zérus várható értékű fehérzaj folyamatot tételezünk fel. Vektoros lineáris tárgyalásban a feltételes várható érték és a kaotikus viselkedéssel kapcsolatos zajfolyamat merőlegesek egymásra, ami lehetővé teszi a nem megjósolható, kaotikus rendszerek egyszerű tárgyalását. A feltételes várható érték vektor merőleges a becslési hibára. Exponenciális vagy geometriai eloszlásnál a folyamatok múltja és jelene merőleges a jövőjükre.
/ CHAOS THEORY: Chaotic systems are by definition systems with unpredictable behavior, memoryless systems. The already known chaotic systems are deterministic, labile systems, their behavior depends on the initial value, and after a finite time their behavior becomes chaotic and unpredictable. The chaotic behavior is an internal (immanent) property of chaotic systems, and chaotic behavior can only be described by probabilistic, stochastic means. New chaotic systems, e.g. related to waiting times, random walk problems, random numbers, random graphs, are described by the concepts of memorylessness, unpredictable behavior, and independent incremental, additive processes. In memoryless systems, the future of the eternally young process is independent of the present and past of the process, which have exponential or geometric distributions. Stochastic processes with independent increments are called memoryless, unpredictable processes. Chaotic systems are often related to the length of lifetimes, waiting times, and generally random periods of time until some event occurs.
In the normal distribution, the expected value and the standard deviation are independent quantities, while at the uniform distribution, the zero expected value and the standard deviation, the range, are independent. In the Kalman filter, a white Gaussian process with zero expected value, or a white noise process with zero expected value, is assumed. In vector linear analysis, the conditional expected value and the noise process associated with chaotic behavior are perpendicular to each other, which allows for a simple discussion of unpredictable, chaotic systems: the conditional expected value vector is perpendicular to the estimation error. In an exponential or geometric distribution, the past and present of the processes are perpendicular to their future.
.
BEVEZETÉS
Az ismert káoszelmélet (https://hu.wikipedia.org/wiki/K%C3%A1oszelm%C3%A9let) olyan nemlineáris determinisztikus időfüggő és labilis rendszerekkel foglalkozik, amelyek viselkedése csak részben jelezhető előre, a determinisztikus törvényszerűségek ellenére. A tekintett labilis rendszerek érzékenyek a kezdőfeltételekre, amit pillangóhatásnak is neveznek. A labilis determinisztikus rendszerek részben statisztikus, sztochasztikus módszerekkel írhatóak le,
A valódi determinisztikus rendszerek esetén az aszimptotikus viselkedés t = végtelenben is egyértelműen határozott, azaz csak a részben determinisztikus labilis rendszerek viselkedhetnek kaotikusan. A kevés állapotjelzővel leírható determinisztikus rendszerek is mutathatnak megjósolhatatlan viselkedést. Például a kettős inga mozgása egy idő után függetlenné válik a kezdeti állapotától, nem tér vissza a kezdeti állapotába, strukturálisan labilis rendszer:
A kettős inga két, egymáshoz csatolt ingából álló egyszerű fizikai rendszer, melynek kaotikus mozgását kezdetben determinisztikus differenciálegyenletek határozzák meg, mégis a mozgása egy idő után véletlenszerű, kaotikus.Több változata van, a két inga hossza és tömege is lehet megegyező, vagy különböző. A mozgás leírása lehet 3 dimenziós és 2 dimenziós is (https://scienceworld.wolfram.com/physics/DoublePendulum.html).

A kaotikus viselkedést mutató rendszerek részben determinisztikus rendszerek, ellentétben a káosz szó jelentésével, ami teljes rendezetlenséget (függetlenséget, megjósolhatatlanságot, memórianélküliséget) jelent. Véges idő után instabilitás, lokális rendezetlenség, véletlen viselkedés jellemzi a tekintett rendszereket. A viselkedés akkor labilis, ha két, egymáshoz közeli kezdőhelyzetből indítva a rendszerállapotok különbségei véges időben modellezhetetlenül, kiszámíthatatlanul nőnek. Edward Lorenz egy 1963-as cikkében felismerte a nemlineáris rendszerekben lehetséges nagy érzékenységet a kezdeti feltételek kis eltéréseire. Egyik előadásának a címe alapján sokszor a pillangóhatásként idézik a jelenséget: Predictability: Does the flap of a butterfly's wings in Brazil set off a tornado in Texas? („Megjósolhatóság: Vajon egy pillangó szárnycsapása Brazíliában okozhat-e tornádót Texasban?”). Kis eltérés a kezdeti feltételekben modellezhetetlen nagy változást okoz egy labilis -bizonytalan egyensúlyi állapotú- rendszer állapotában, ezért a viselkedésük hosszú távú előrejelzése lehetetlen, ami a labilis rendszerek alaptulajdonsága.
Létezik a fizikának egy kvantumkáosz-elméletnek nevezett területe, a káoszelmélet egy másik fejezete, amely a kvantummechanika törvényeit követő nemdeterminisztikus rendszerekkel foglalkozik (https://hu.wikipedia.org/wiki/K%C3%A1oszelm%C3%A9let). Egy további új fejezete a káosz elméletnek, amikor a rendszerek viselkedése megjósolhatatlan, és a rendszerek kizárólag statisztikai, valószínűségelméleti módszerekkel írhatóak le, a következőkben ismertetjük.
Megj,: a kauzális és a kaotikus rendszerek memóriájáról: Az irodalomban memórianélküli egy rendszer, ha a kimenet csak a bemenet függvénye. Pl. az elektromos ellenállások memória nélküli elemek. A kauzális rendszerek leírása impulzusválasszal (Dirac-delta) lehetséges. Az ok-okozati összefüggés memória nélküli rendszerekkel
KAOTIKUS, MEGJÓSOLHATATLAN VISELKEDÉSŰ FOLYAMATOK
A kaotikus vagy memórianélküli rendszereknél az ok-okozati összefüggésről: a rendszer kimenete definíció szerűen nem függ a jelen és múltbeli ki- és bemenetektől, ami kaotikus, memórianélküli rendszerek alaptulajdonsága. Ha a jövő csak a jelenétől függ, de a múlttól nem, akkor Markov lánccal írható le a rendszer, az egy lépéses memóriájú rendszerek a véges Markov láncokkal. Legyen egy rendszer állapothalmaza: s1, s2, …, sr. … . A rendszer az si állapotból az sj állapotba pij valószínűséggel lép, ahol pij az átmeneti valószínűség P mátrix egyik eleme. A P mátrix a rendszer egylépéses memóriája.
Az eloszlások között csak a geometriai és az exponenciális eloszlások memória nélküliek, örökifjú tulajdonságúnak nevezik a valószínűségszámításban. Diszkrét esetben
a geometriai eloszlás definíciója az első sikeres kísérletet írja le független és azonos eloszlású Bernoulli-próbák végtelen sorozatában, például az érmefeldobásnál. Folytonos esetben a memórianélküliség, az örökifjú tulajdonság olyan véletlen jelenségeket modellez, mint például a két földrengés közötti idő. A memórianélküliség, az örökifjú tulajdonság alapján a korábbi sikertelen kísérletek száma vagy az eltelt idő független, nincs hatással a jövőbeni kísérletekre vagy az túlélési időre. A túlélési idő definíciója: S(t) = P (X>t), ahol S(t) annak a valószínűsége, hogy él, ha X = t -ben életben volt. Ekkor igaz, hogy S(kt) = S(t)k vagy S(t/k) = S (t)1/k , ahol k pozitív valós. Következik, hogy S(t) = S (1)t = exp (t ln S(1) = exp (-λt), ahol λ = -ln S (1) ≥ 0, azaz exponenciális eloszlású a rendszer. A geometriai az egyetlen diszkrét memória nélküli eloszlás, az exponenciális az egyetlen folyamatos memória nélküli eloszlás, továbbá egyben maximális entrópiájú eloszlások. A zérus várható értékű egyenletes eloszlás és a normális eloszlás a várható értékek és a szórásnégyzetek függetlensége miatt fontos független növekmény folyamatok.
A memórianélküli, megjósolhatatlan (= kaotikus, örökifjú eloszlású) folyamatok korrelálatlan, független növekményű folyamatok, bár a korrelálatlanság csak lineáris függetlenséget jelent. A független növekményű folyamatot homogénnek nevezünk, ha a ξ(t1)-ξ(t0) eloszlását csak a t1 - t0 intervallum hossza határozza meg, és független a t0 -tól. Az egyszerűség kedvéért mindenhol feltételezik, hogy ξ(0)=0, és feltételezik a homogenitást is.
Véletlen növekményű, additív kaotikus folyamatok: a valószínűségelméletben a Lévy-folyamatok, vagy folytonos additív folyamatok olyan folytonos és sztochasztikus folyamatok, amelyek független, stacionárius növekményűek. Az egymást követő növekmények véletlenszerűek, amelyekben a páronként különálló időintervallumokban a növekmények függetlenek, és az azonos hosszúságú különböző időintervallumokban a növekmények azonos valószínűségi eloszlásúak. A Lévy-folyamat a diszkrét véletlen bolyongás folytonos idejű analógonjának tekinthető. A Lévy-folyamatok legismertebb példái a normális eloszlással kapcsolatos Wiener-folyamat, és az egyenletes eloszlással https://en.wikipedia.org/wiki/Independent_increments, kapcsolatos Brown-folyamat. Ha a t1 - t0 intervallum hossza exponenciális eloszlású, ekkor a folyamat Poisson vagy gamma-folyamat. (A független növekményű folyamatok osztálya feltehetően csak az elmlített néhány kaotikus folyamatot tartalmazza, diszkrét esetben a geometriai eloszlást is,).
Diszkrét esetben is az additív sztochasztikus folyamatok független, stacionárius növekményűek, és
- az egyenletes eloszlású növekmény folyamatok összege normális eloszlású, az egyenletes eloszlás mintázatai geometrikus eloszlásúak, (ha az eseményeinek egyenletes eloszlásúak, 1/b értékűek, b az elemi események száma, akkor a független elemi események valamely tetszőleges k hosszú (k=1,2,3,...,kmax) mintázatának geometriai valószínűsége (b-1)/bk ),
- a normális eloszlású növekmény folyamatok diszkrét Brown folyamatok, a pénzügyi folyamatok hasonlóak,
- a geometriai eloszlású növekmény folyamatok negatív binomiális eloszlású folyamathoz vezetnek. pl. bolyongással, élettartamokkal kapcsolatosak,
- az exponenciális eloszlású növekmény folyamatok, és a származtatott a Poisson, pl. az Erlang eloszlások.
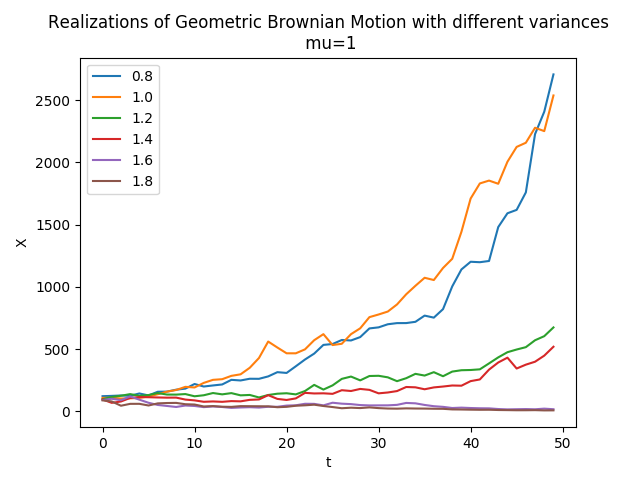
A matematikában a Wiener-folyamat pl. bolyongási problémákkal (https://hu.wikipedia.org/wiki/V%C3%A9letlen_bolyong%C3%A1s) kapcsolatos. A folyamat egy Norbert Wiener által felfedezett valós értékű, folytonos vagy diszkrét idejű független normális eloszlású növekményekkel rendelkező sztochasztikus folyamat, ahol a növekmények zérus várható értékű normális eloszlásúak, és amelynek a derivált folyamata a fehérzaj folyamat. Gyakran előfordul alkalmazott matematikában, a közgazdaságtanban, a kvantitatív pénzügyekben, az evolúciós biológiában és a fizikában. A Wiener-folyamat  tulajdonságai:
tulajdonságai:

 t független növekményű folyamat, azaz minden
t független növekményű folyamat, azaz minden  a növekmény
a növekmény 
 független a múltbeli értékektől, egy folyamat független növekményű, ha 0 ≤ s1 < t1 ≤ s2 < t2 akkor Wt1 − Ws1 és Wt2 − Ws2 független valószínűségi változók.
független a múltbeli értékektől, egy folyamat független növekményű, ha 0 ≤ s1 < t1 ≤ s2 < t2 akkor Wt1 − Ws1 és Wt2 − Ws2 független valószínűségi változók. t növekményei normális eloszlásúak,
t növekményei normális eloszlásúak,  zérus várható értékű, u szórású normális eloszlású:
zérus várható értékű, u szórású normális eloszlású: 
 t folytonos esetben:
t folytonos esetben:  majdnem biztosan folytonos t -ben.
majdnem biztosan folytonos t -ben. 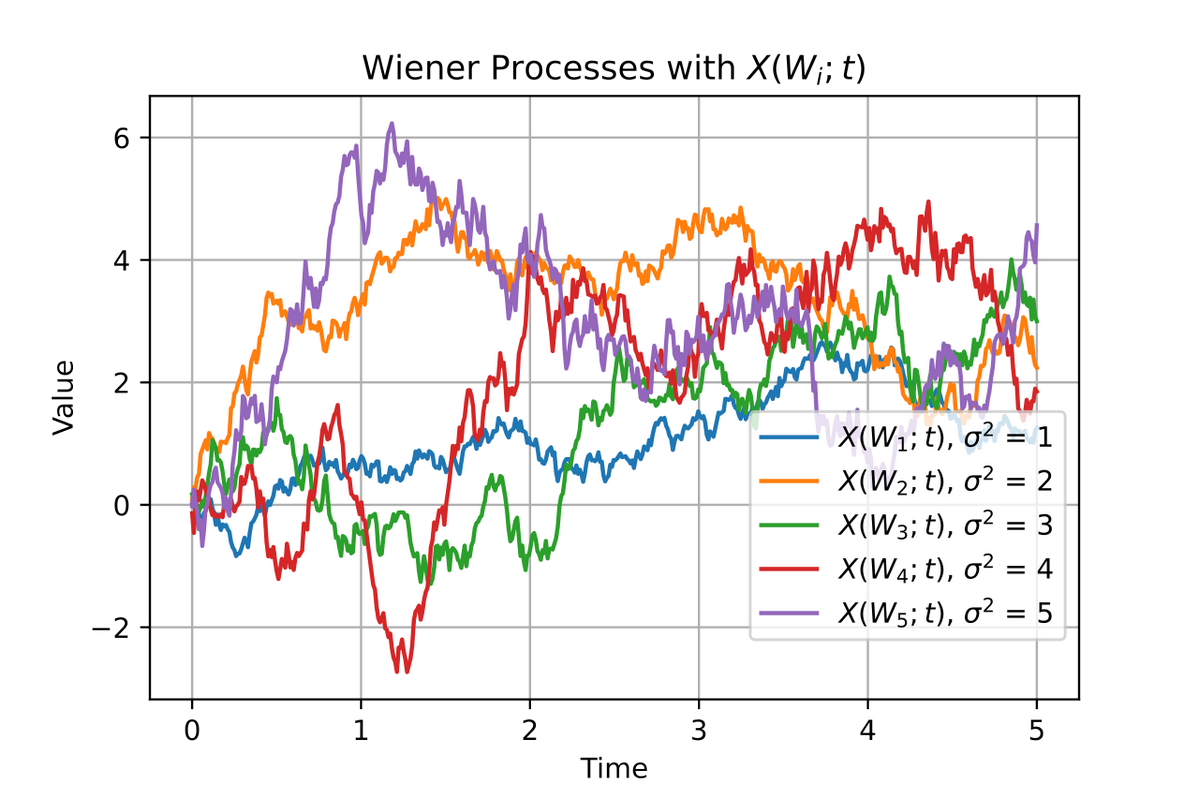
- (https://en.wikipedia.org/wiki/Wiener_process)
A fehér zaj (amely a Wiener folyamat derivált folyamata, nincs memóriája, matematikai szerepe fontos, a valóságban nem létezik) olyan zaj, melynek teljesítménysűrűsége független a frekvenciától, (https://hu.wikipedia.org/wiki/Feh%C3%A9rzaj). Bár a fehérzaj korrelálatlan folyamat, és független növekményű, elenyésző az esélye, hogy hosszú zérus növekményű intervallumokat kapjunk, de valahol 1 valószínűséggel előfordulhatnak egy nem megszámlálhatóan végtelen végtelen folyamatban. A valóságban nem létezik végtelen sávszélességű fehérzaj, mert végtelen lenne a teljesítménye, ezért zérus várható értékű és sávkorlátozott fehérzajt tételezünk fel. Zérus várható értékű fehérzaj esetén a szórásnényzet szabadon választható. Numerikus szimulációk esetén a mintavételezésnél a felső határfrekvencia a mintavételi frekvencia fele. Fizikai jelenségek modellezésénél a Wiener folyamat a fontosabb.
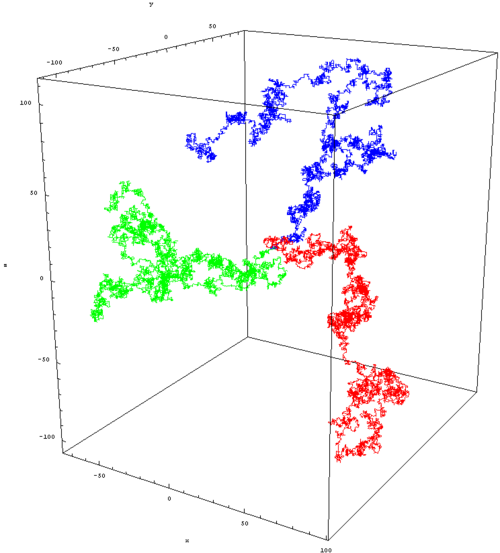
Bolyongási problémák: A fizikában a Brown-mozgás (https://en.wikipedia.org/wiki/Geometric_Brownian_motion) a gázokban és folyadékokban lebegő (szuszpendált) részecskék szüntelenül zajló, véletlenszerű hőmozgása a legismertebb, amelyet Robert Brown angol botanikus fedezett fel vízben elkevert virágporszemcséket vizsgálva, a mozgás az anyag atomos szerkezetének fontos bizonyítéka volt. A káoszelméletben szereplő globális keveredés egyik jó példája, amely szerint tipikus kezdőfeltételekkel indítva kellően hosszú idő alatt a rendszer az összes lehetséges állapothoz közel kerül. A szuszpendált részecskék mozgásuk során állandó ütközéseket szenvednek el, viselkedésüket a Maxwell-féle sebességeloszlási függvény írja le. A Brown-mozgás trajektóriái általánosságban véletlenszerű, folyamatos és rendszertelen pályavonalak. A Brown mozgás nem korrelálatlan, mert a részecske adott időpillanatbeli helye függ attól, hogy az előző pillanatban hol volt. A Brown-mozgás egy független növekményű folyamat, ami azt jelenti, hogy a részecske adott helyzete csak az előző pillanatbeli helyzetétől függ, és az azt megelőző helyzetektől független. A Brown-mozgás jellegzetessége, hogy a folyamat nem stacionárius, a kezdeti helyétől az idő vagy a lépésszám négyzetgyökével arányosan távolodik.
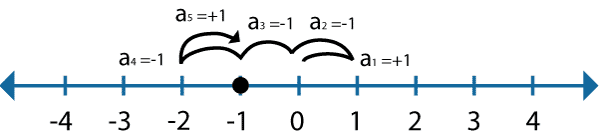
Bolyongás az egész számokon véletlen lépésekkel
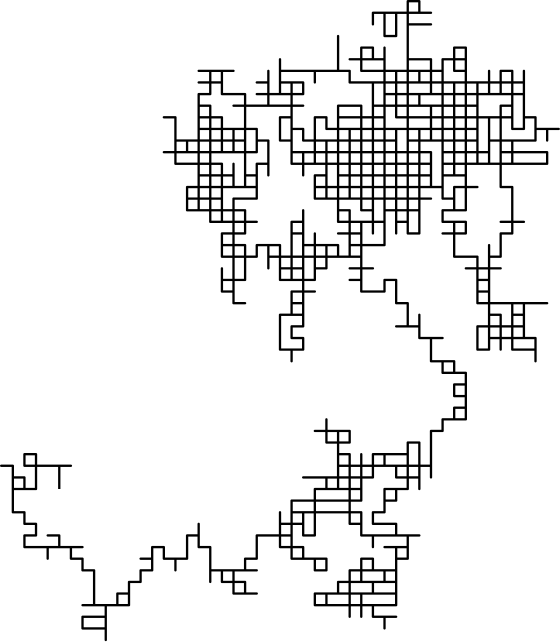
A véletlen bolyongás az a folyamat, amikor véletlenszerűen mozgó tárgyak elvándorolnak onnan, ahonnan indultak. Véletlen bolyongás sokféle van, pl. egy olyan sztochasztikus folyamat, amely az egész számokon véletlen lépésekből áll, amely 0-nál kezdődik, és minden lépésnél egyenlő valószínűséggel +1 vagy −1 lépést tesz a számegyenesen. További példa egy molekula nyomvonala, miközben folyadékban vagy gázban halad (lásd a Brown-mozgást), a táplálékot kereső állat keresési útvonala, az ingadozó készletek árai, és egy szerencsejátékos pénzügyi helyzete. Sok folyamatot lehet modellezni véletlenszerű bolyongási modellek segítségével, még akkor is, ha a ezek a jelenségek valóságban nem feltétlenül véletlenszerűek. A kezdeti helytől a távolság a lépésszám négyzetgyökével arányosan távolodik (https://en.wikipedia.org/wiki/Random_walk). A távolság a lépésszám négyzetgyökével osztva egy állandóhoz, (2/π)1/2 -hoz tart.
A képen 7 fekete pont látható, amelyek egy helyről indulnak változó lépésnagysággal két dimenzióban. Erdős Pál és Samuel James Taylor kimutatta 1960-ban, hogy 4-nél kisebb vagy egyenlő dimenziók esetén bármely két adott pontból induló két független véletlenszerű séta szinte biztosan végtelenül sok metszésponttal rendelkezik, 5-nél nagyobb dimenzióknál viszont szinte biztosan csak véges gyakran metszik egymást. A kétdimenziós véletlenszerű séta aszimptotikus függvényét a lépések számának növekedésével egy Rayleigh-eloszlás adja meg.
Bolyongás egy dimenzióban, amikor a lépésnagyságokat véletlen számok határozzák meg, és a lépések irányai is véletlenszerűek. A kérdés az, hogy mekkora a valószínűsége annak, hogy nagy t idő után valamilyen távolságban található a mozgó objektum? Mikor helyettesíthető a véletlen lépésnagyság a várható értékével? Ha minden lépést a 0 várható értékével helyettesítünk, akkor várhatóan helyben marad. H a lépések összegének a négyzetes várható értékét számítjuk, akkor a távolság a lépésszám négyzetgyökével távolodik.
Három dimenziós bolyongás, 1921-ben Pólya György bebizonyította, hogy 3 vagy annál nagyobb dimenzió esetén a dimenziók számának növekedésével csökken annak valószínűsége, hogy visszatér a mozgás az Origóba. 3 dimenzióban a valószínűség nagyjából 34%-ra csökken. (https://en.wikipedia.org/wiki/Random_walk)
Magasabb dimenziókban a véletlenszerűen meglátogatott pontok halmazát diszkrét fraktál-nak nevezik , egy olyan halmaznak, amely sztochasztikus önhasonlóságot mutat, folytonos esetben látványos ábrákat eredményez. (https://hu.wikipedia.org/wiki/Mandelbrot-halmaz). A véletlen bolyongás pályája a meglátogatott pontok halmaza, figyelmen kívül hagyva, hogy a bolyongás mikor látogatta meg a pontot.
Amikor gradienssel mérhető, hogy mennyit változik a részecskék Brown-féle hőmozgása (egysége darab/ térfogat), amikor az egyik régióból a másikba mozognak:
Brown-mozgás két dimenzióban, gázokban, folyadékokban, amikor a hőmérséklet gradiense még nem nulla
Függetlenség, Markov folyamatok, az örökifjú tulajdonság
A korreláció méri két tetszőleges érték közötti lineáris kapcsolat erősségét. A korrelálatlanság nem feltétlenül jelent függetlenséget, de bizonyos, hogy nincs az értékek között lineáris összefüggés. Ha két véletlen mennyiség korrelációja nulla, akkor korrelálatlanok, és a kapcsolatot feltételes valószínűségekkel írjuk le. A normális eloszlású valószínűségi változókra jellemző, hogy ha korrelálatlanok, akkor függetlenek is. A zérus várható értékű egyenletes eloszlású valószínűségi változók szórásai (terjedelmei) tetszőleges értékűek lehetnek, A korreláció alkalmazható fehér zaj vagy normális eloszlású forrászajú változók közötti kapcsolat erősségének elemzésére.
A feltételes várható értéket a valószínűségszámításban (https://en.wikipedia.org/wiki/Conditional_expectation) a feltételes valószínűség definiálására használják. A feltételes várható érték lehet valószínűségi változó vagy függvény, amelyet feltételes valószínűségi eloszlással számítanak, vagy például a folyamat jövőjéből képzett vektorának a folyamat múltjára történő vetítésével, pl. a realizációelméletben, a káoszelméletben zérus, esetleg konstans. Ha a valószínűségi változó csak véges számú értéket vehet fel, akkor a "feltétel" az, hogy a változó ezeknek az értékeknek csak egy részhalmazát veheti fel. Formálisan, abban az esetben, ha a valószínűségi változó egy diszkrét valószínűségi téren lett definiálva, a "feltételek" ennek a valószínűségi térnek a partíciói. A Kálmán-szűrőnél, amely egy feltételes várhatóérték számítás: a kimenőjelről jelről feltesszük, hogy zérus várható értékű, és bizonyítható, hogy amennyiben a zajok független normális, azaz fehér Gauss-folyamatok, illetve fehér zajok, azaz független egyenletes eloszlású zajfolyamatok, akkor Kálmán-szűrő becslése optimális legkisebb négyzetes LSQ) becslés, és az LSQ, MLH és Bayes becslések egybeesnek, mert zérus várható érték esetén a szórásnégyzet (terjedelem) tetszőleges értékű lehet.
Függetlenség: az elemi események halmaza páronként független, ha két esemény együttes bekövetkezésének valószínűsége a két esemény valószínűségeinek szorzata, vagy egy másik meghatározás szerint: egy esemény feltételes valószínűsége az esemény valószínűségével egyenlő. A nem együttesen bekövetkező, egymás utáni események sorozatot alkotnak. A sorozatokban az elemi események ismétlődnek, ekkor a függetlenség definíciója: ha egy esemény (vagy elemek) bekövetkezése csak a legutolsó eseménytől, elemtől függ, és az előzőektől független, akkor sorozat Markov folyamat. Ha egy esemény (vagy elem) bekövetkezése nem függ sem a múltjától, sem a jelenétől, akkor a folyamat nem megjósolható, memórianélküli kaotikus folyamat, és lehet exponenciális vagy geometriai eloszlású
Tehát: A kaotikus, megjósolhatatlan rendszerek esetén a rendszerleírásra használt eloszlások a normális, az egyenletes, a geometriai és az exponenciális eloszlások, és az ezekből származtatott eloszlások, folyamatok. A normális eloszlásnál a várható érték és a szórásnégyzet független mennyiségek, az egyenletes eloszlásnál, ha zérus a várható érték, a szórás (a terjedelemből számolva) értéke tetszőleges lehet. A geometriai és az exponenciális örökifjú, emórianélküli tulajdonságúak, azaz a folyamat jövője független a folyamat jelenétől és a múltjától*. Megj,.: Kevés geometriai folyamattal lehet találkozni az irodalomban, pedig a véletlen számoknál hasznos.
A Markov folyamatoknál csak a folyamat jelenétől függ a folyamat jövője. A Markov-folyamat kifejezés egy sztochasztikus folyamat részben emlékezet nélküli tulajdonságára utal, ami azt jelenti, hogy jövőbeli fejlődése független a történetétől, csak a jelenétől függ. Nevét Andrej Markov orosz matematikusról kapta. Az erős Markov-tulajdonságnál a „jelen” jelentését egy leállási időként ismert valószínűségi változóval határozzuk meg. A Markov féle véletlen mező kiterjeszti a tulajdonságot két vagy több dimenzióra.
Eloszlások, példa folyamatok
Az exponenciális eloszlás sokszor használható véletlen időtartamok modellezésére:
- egy üzletben két ügyfél érkezése közötti idő,
- egy számítás elvégzése egy számítógépen,
- forgalmi helyzeteket leíró elmélet,
- egy ember reakcióideje,
- két esemény bekövetkezése között eltelt idő pl. izzólámpák esetén (megbízhatóságelmélet),
- járványterjedés modellezése, egy fertőzés terjedése, de a gyógyulási időt is,
- radioaktív részecskék bomlási ideje,
- az exponenciális eloszlású független valószínűségi változók összege Γ-eloszlású. Pontosabban ha X1, X2, … Xn független, λ paraméterű exponenciális eloszlású valószínűségi változók, akkor X1 + X2 + … + Xn n rendű, λ paraméterű Γ-eloszlású valószínűségi változó.
A Poisson folyamat (https://hu.wikipedia.org/wiki/Poisson-folyamat) egy örökifjú sztochasztikus folyamat**, mely események számát és időközeit modellezi, amelynél a T1, T2, . . . érkezések közötti időintervallumok exponenciális eloszlású független valószínűségi változók. Alapfolyamata egy időben folytonos számláló folyamat {N(t), t ≥ 0}, a következő tulajdonságokkal: N(0) = 0, egymástól független növekmények jellemzik, továbbá stacionárius növekmények (bármely időközben az előfordulások számának eloszlása csak az időközök hosszától függ), és nincsenek egyidejű események. A következő esemény várakozási ideje exponenciális eloszlású. Memória-mentesség, az örökifjú tulajdonság jellemzi az eloszlást, azaz az egymás utáni beérkezési események függetlenek, és egy t időbeli eseményt nem befolyásolja a t idő előtti események bármelyike. Alkalmazásai:
-telefonhívások beérkezése,
- labdarúgó meccseken előforduló gólok,
- webszerverekhez beérkező kérelmek.
- részecske-emisszió radioaktív bomláskor (ami inhomogén Poisson-folyamat),
- a sorbanállás elméletben az ügyfelek-kiszolgálók sorbaállása sokszor Poisson-folyamat. A sorbanállás elméletben a legkorábbi, Erlang -féle modellben (https://hu.wikipedia.org/wiki/Sorban%C3%A1ll%C3%A1s-elm%C3%A9let) a legkorábbi, Erlang -féle modellben a beérkezések a Poisson-folyamat szerint történnek, a kiszolgálás idő egy határozott érték, a kiszolgálók száma a sorbanállási csomópontokon több mint 1 (k = 1, 2,...). A Poisson-folyamat a véletlenszerű eseményeket memóriamentes folyamatként kezeli, a különböző időintervallumoknál nem veszi figyelembe, hogy korábban mi történt. Hasonló az exponenciális eloszlás is, a P folyamat exponenciális változók összegének folyamata.
- egy megadott esemény előtti várakozási idők elemzésénél,
- forgalmi helyzeteket leíró elmélet,
- készülékek és alkatrészek élettartamának meghatározása,
- várakozási idő meghatározására az első meghibásodásig
- gyakori események számának meghatározása két egymástól független ritka esemény között;
- alkalmazási területek például a készülékek megbízhatóságának vizsgálata,
- biztosítási matematika,
- adatátvitel hibaarányának meghatározása,
- a geometriai eloszlás a független Bernoulli-kísérletek eloszlása. A geometriai eloszlás általánosítása a binomiális eloszlás több sikeres kísérletre, amit két módon fogalmaznak meg: vagy az r-edik sikeres kísérletre várnak, vagy azt emelik ki, hogy az r-edik sikeres kísérletre n próbálkozásra volt szükség.
- a geometriai eloszlás az r=1 paraméterhez tartozó negatív binomiális eloszlás, az utóbbi jól közelíti a Poisson eloszlást is speciális esetben. A független geometrikus eloszlású valószínűségi változók összege, amennyiben mindegyiknek ugyanaz a paramétere, negatív binomiális eloszlású, de a negatív binomiális eloszlás nem örökifjú eloszlás.
Például a sorbanállás elméletben a vállalkozások logisztikájának elemzése geometriai eloszláshoz is vezet. A raktárak sorbaállási elméletet alkalmaznak a csomagok raktárból a vevőhöz történő szállítása során a rendszer egyenletes működésének biztosítására. Ekkor a vizsgált sor olyan dobozokból áll, amelyek arra várnak, hogy az ügyfeleknek kiszállítsák. A sorbanállási elmélet alkalmazásával a vállalkozások hatékonyabb rendszereket, folyamatokat, árképzési mechanizmusokat, személyzeti megoldásokat és érkezéskezelési stratégiákat fejleszthetnek ki az ügyfelek várakozási idejének csökkentése és a kiszolgálható ügyfelek számának növelése érdekében (https://hu.wikipedia.org/wiki/Sorban%C3%A1ll%C3%A1s-elm%C3%A9let) .
A műszaki tudományok kaotikus rendszerekkel kapcsolatos egyik területe a megbízhatóságelmélet, ahol kezdetben a műszaki megbízhatóság fogalmát a hibamentes működés (exponenciális eloszlású) valószínűségével azonosították (pl. az első meghibásodásig működő berendezések).
A megbízhatóságelmélet már magába foglalja a hibamentesség, a tartósítás az élelmiszeriparban, a karbantartás és a tárolhatóság fogalmait is. (Néhány oldal a témában:
Meghibásodási gyakoriság (FR: failure rate): Megadja, hogy egy adott darabszámból álló vizsgált rendszer átlagosan hányszor hibásodik meg.
Mértékegysége 1/óra,(FIT – Failures In Time – valamennyi óra alatt átlagosan bekövetkező meghibásodások száma).
Meghibásodások közötti átlagos időköz (Mean Time Between Failures, MTBF): Megadja, hogy a rendszer két meghibásodása között átlagos időt.
Átlagos javítási idő (Mean Time To Repair, MTTR): megadja, hogy a rendszer meghibásodása utáni üzembeállítása átlagosan mekkora időt vesz igénybe.
A megbízhatóságelmélet fontos összetevői:
Működőképesség (reliability),
Rendelkezésre állás (availability),
Biztonság (safety),
Karbantarthatóság, javíthatóság (maintenability),
Tesztelhetőség (testability),
Áttekinthetőség, megismerhetőség (recognizability),
Kezelhetőség (operability),
Védettség, ellenálló képesség (security),
Hihetőség (creditability),
Teljesítmény (performability),
Hitelesség (integrity).
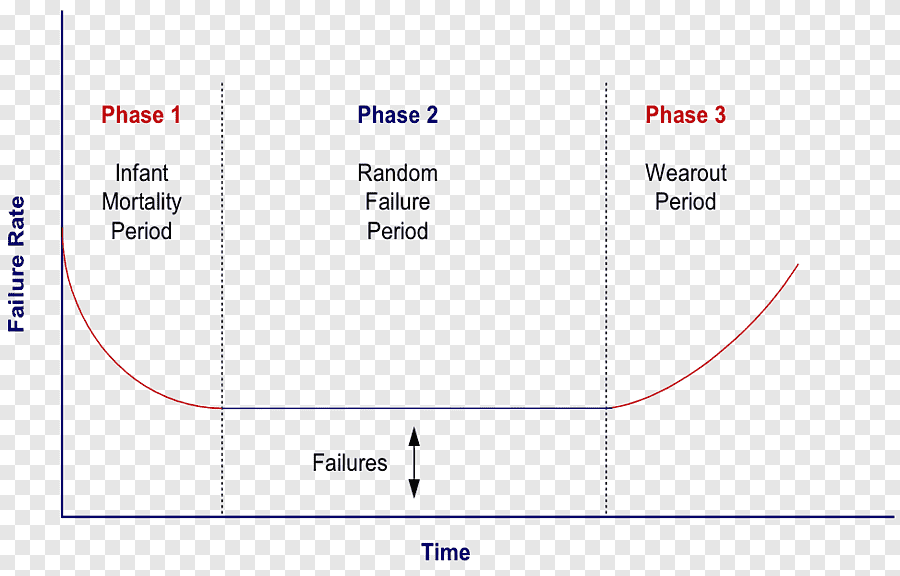
Az első szakaszban a termék korai, esetleg szállítási hibák ideje, ahonnan a hibák száma folyamatosan csökken, és állandósul a hibagyakoriság. A harmadik szakasz az öregedés ideje, amikor az elhasználódás miatt nőni kezd a meghibásodási ráta. Sok kereskedelmi forgalomban lévő termékre jellemző a "fürdőkádgörbe", például a háztartási gépekre. (https://hu.wikipedia.org/wiki/F%C3%BCrd%C5%91k%C3%A1dg%C3%B6rbe)
A Weibull-eloszlás (https://hu.wikipedia.org/wiki/Weibull-eloszl%C3%A1s) általánosan használt eloszlás a megbízhatóságelméletben, egy speciális exponenciális eloszlás, az időfüggő meghibásodások hatványfüggvénnyel való megközelítésére szolgál, amivel a “fürdőkádgörbe” korai és elhasználódással kapcsolatos szakaszai, illetve az ezekkel kapcsolatos meghibásodások is jól közelíthetőek és számszerűsíthetőek. A meghibásodás-mentes működés valószínűsége egy (t, t+Δt) időintervallumban független a korábban eltelt időtől, és csak a Δt időintervallum nagyságától függ, azaz a jövőbeni meghibásodás független a rendszer előéletétől. Weibull szerint a túlélés valószínűsége: R(t) = exp -(t/β - γ/β)α , ahol az eloszlás paraméterei:
α - alakparaméter vagy Weibull kitevő, amely a Weibull eloszlás görbéjének alakját határozza meg:
– α<1: a korai meghibásodások szakasza, a meghibásodási ráta értéke az idő függvényében monoton csökken;
– α=1: a véletlen meghibásodások, a használati idő szakasza, a meghibásodási ráta értéke az idő függvényében állandó;
– α>1: az elhasználódással összefüggő meghibásodások szakasza, a meghibásodási ráta értéke az idő függvényében monoton nő;
β - az ún. karakterisztikus élettartam;
γ - a helyzetparaméter, amely a meghibásodások megkezdődésének időpontját határozza meg:
– γ>0: olyan üzemállapot, amelyben a meghibásodások csak egy t= γ idő után kezdődnek meg (pl. korrózió, dugaszcsatlakozók felületén bevonat képződése),
– γ=0: olyan üzemállapot, amelyben a meghibásodások már az igénybevétel kezdetén fellépnek.
A Weibull eloszlás egy másik változata (https://hu.wikipedia.org/wiki/Weibull-eloszl%C3%A1s) szerint x valószínűségi változó valószínűség-sűrűségfüggvénye:

ahol k > 0 az alakparaméter és λ > 0 a skálaparaméter. A Weibull-eloszlás*** több más valószínűségi eloszlással is kapcsolatos, pl. az exponenciális eloszlással (k = 1), és a Rayleigh-eloszlással (k = 2). A Weibull-eloszlás ez utóbbi kettő között egy interpolációnak tekinthető. Ha x az az érték, mely a meghibásodásig eltelt időt jelzi, akkor a Weibull-eloszlás az idővel arányos meghibásodási gyakoriságot jelzi. A k alakparaméter értelmezése:
- k<1 azt jelenti, hogy a meghibásodási gyakoriság idővel csökken. Ez akkor fordul elő, ha a kezdeti meghibásodás jelentős, és idővel ezért csökken a meghibásodás, mert a potenciálisan hibás elemek már kiestek a rendszerből.
- k=1 esetén a meghibásodási gyakoriság időben állandó. Ez azt jelenti, hogy a hibákat véletlenszerű külső események okozzák.
- k>1 azt jelzi, hogy a meghibásodási gyakoriság időben növekszik. Ez akkor fordulhat elő, amikor a vizsgálat tárgya az öregedési tartományba kerül, a rendszer alkotóelemei az elöregedés, és az elhasználódás miatt egyre gyakrabban hibásodnak meg.
Megj.: Az entrópia a hőtan és az informatika fogalma egy rendszer rendezetlenségi fokát jellemzi, a termodinamikában az anyagi rendszerek molekuláris rendezetlenségét és a termodinamikai valószínűségének a mértékét. A rendszerállapotok termodinamikai valószínűségeit jelölje ωi , i = 1,2,3,...,
akkor -k ln ωi az entrópia az ωi állapotban, ahol k a Boltzmann-állandó. Ha egy rendszer a környezetéből nem vesz fel hőt, akkor a rendszerben lejátszódó spontán folyamatok során a rendszer entrópiája mindaddig nő, amíg egyensúlyi állapotba jut, és egyensúlyi állapotában a rendszer entrópiája maximális. A termodinamika második törvénye kimondja, hogy az izolált rendszer entrópiája nem csökken. Egy nyílt rendszer entrópiája csökkenhet, de az Univerzum teljes entrópiája nem. Ha egy folyamat reverzibilis, az entrópia nem változik, míg a visszafordíthatatlan folyamatok mindig növelik a teljes entrópiát. A termodinamikai entrópia fogalmát Rudolf Clausius vezette be. (Tisztelet illeti Boltzmannt a logaritmikus függés bevezetéséért!) Formai hasonlóság alapján Neumann János javasolta Shannonnak, hogy az informatika alapképletét nevezze entrópiának (https://hu.wikipedia.org/wiki/Shannon-entr%C3%B3piaf%C3%BCggv%C3%A9ny). Bizonyított, hogy az exponenciális eloszlás családban a geometriai és az exponenciális eloszlások entrópiája maximális. Az exponenciális eloszlás családra vonatkozóan ld. https://en.wikipedia.org/wiki/Exponential_distribution .
Vektoros tárgyalásban a feltételes várható érték és a kaotikus viselkedéssel kapcsolatos zajfolyamat* merőlegesek egymásra, ami lehetővé teszi a nem megjósolható rendszerek egyértelmű matematikai tárgyalását, leírását. A Bayes becslés (https://hu.wikipedia.org/wiki/Bayes-f%C3%A9le_rekurz%C3%ADv_becsl%C3%A9s) esetén pedig számszerűsíthetőek az a priori és posteriori valószínűségek. Ha a változók normál eloszlásúak és az átmenetek lineárisak, a Bayes-becslés és a Kálmán-szűrővel számított feltételes várható érték megegyeznek, és az állítás általánosítható zérus várható értékű egyenletes eloszlású fehérzajra is. A feltételes várható érték merőleges a becslési hibára, míg az exponenciális vagy geometriai eloszlásnál a folyamatok múltja és jelene merőleges a jövőjükre. Természetes cél volt a tárgyalás, azaz az örökifjú, memórianélküli rendszerek, a független növekményű folyamatok, a feltételes várható érték számításán alapuló vetítés, és a bolyongások tárgyalásának egyesítése. Az a közös bennük, hogy a folyamat múltját és jelenét ismerve semmit sem lehet állítani a folyamat jövőjéről (a várható értéken és a szóráson kívül), ami az örökifjú, a memórianélküli tulajdonság, a független növekmények miatt. Egy független növekményű folyamatot homogénnek nevezünk, ha a ξ(t1)-ξ(t0) eloszlását csak a t1 - t0 intervallum hossza határozza meg, és független a t0 -tól, és az egyszerűség kedvéért mindenhol feltételezik, hogy ξ(0)=0. Néhány olyan sztochasztikus folyamat, amely definíció szerint rendelkezik független növekményekkel, a Wiener-folyamat, a fehér zaj, az összes Lévy-folyamat, az összes additív folyamat, és a Poisson-pontfolyamat. Miért hagyják ki a geometriai folyamatokat (v.ő. diszkrét Brown mozgás)? (https://en.wikipedia.org/wiki/Independent_increments).
MEMÓRIANÉLKÜLI, ÖRÖKIFJÚ PROBLÉMÁK
Egy dimenziós eset-ben diszkrét örökifjú sorozatokat fogunk vizsgálni, melyek geometriai eloszlásúak. Ha valamely sorozat eseményeinek, elemei egyenletes eloszlásúak, valószínűségei egyenlőek, 1/b értékűek, ha az elemi események száma b, ami jelölje a számrendszer alapszámát is, akkor a független elemi események valamely tetszőleges k hosszú (k=1,2,3,...,kmax) független sorozatának valószínűsége (b-1)/bk , és geometriai eloszlású. Az eloszlás paramétere (b-1)/b, egyben az egységnyi hosszú sorozatok, a sziglik valószínűsége. Az eloszlás várható értéke is b/(b-1), a valószínűségek összege pedig 1 – b-kmax . A várható érték létezésének feltétele, hogy kmax megszámlálhatóan végtelen legyen.
Megj.: Nem megszámlálhatóan végtelen sorozatok esetén a Haar mérték (https://en.wikipedia.org/wiki/Haar_measure) bináris esetben véges, azaz normálható mérték. Bár a Haar mérték kiszámítása bonyolult, de lényeges állítás, hogy bináris nem megszámlálható esetben is létezik normálható mérték (mert nem megszámlálhatóan végtelen sorozatok esetén a számtani közép és a gyakoriságok általában divergálnak).
Például valakinek a születési dátuma egy véletlen szám, nnhhéé szerkezetben lekérdezhető az https://www.piday.org/find-birthday-in-pi/ oldalon. Egy 2011 január 11.-én született diák születési dátuma a '11·11·11' , és sorozatként a pí szám 51150 számjegyénél kezdődik, a valószínűsége 9 x10-6. A véletlen egybeesés olyan események, körülmények egybeesése, amelyeknek nincs -vagy nem ismert az- okozati összefüggése, és amelyeknek a okszerűnek tekintése hamis állításokhoz, esetleg a fatalizmusba vetett hithez vezethet, az utóbbi szerint az események egybe esése pontosan eltervezett. Statisztikai szempontból az egybeesések törvényszerűek. Példa erre a születésnapi probléma, mely szerint annak a valószínűsége, hogy két embernek egyforma születésnapja van, már meghaladja az 50%-ot egy 23 fős csoportban. (A születésnapi probléma általánosítása: https://www.mdpi.com/2227-7390/12/24/3882: M. Pollanen (2024) A Double Birthday Paradox in the Study of Coincidences, Mathematics 23(24), 3882.) A véletlenek nemcsak a mindennapi életben, hanem a tudományos és statisztikai vizsgálatokban is előfordulnak. A valószínűségszámítás és a matematikai statisztika elegendő az egybeesések magyarázatára: az egymástól független események nem egymást kizáró események, lehet nem zérus az együttes előfordulásuk valószínűsége.
Másik példa: ha adott valamilyen előre rögzített szöveg, és egy majom korlátlan ideig véletlenszerűen ütögeti egy írógép billentyűit, akkor igen kis valószínűséggel, de igen hosszú idő után már majdnem biztosan az adott szöveget is leírja. Az állítás matematikai bizonyítása lehetséges. Cicero így érvelt a De natura deorum-ban: „Aki ebben hisz, az azt is elhiheti, hogy egy zsáknyit a huszonegy betűből földre szórva az Annales lesz olvasható. Kételkedem abban, hogy akár csak egy rövid szakasza is megjelenne.”
(https://hu.wikipedia.org/wiki/V%C3%A9gtelen_sok_majom_%C3%A9s_%C3%ADr%C3%B3g%C3%A9p_t%C3%A9tele).
Cicero jól érezte, hogy az értelmes szöveg megjelenésének csak kis valószínűsége van, és a lehetséges megjelenés a szöveg hosszával fordítva arányos. Tegyük fel, hogy a kérdéses Annales (történelemkönyv) 100 oldal hosszú, oldalankét 100 betűvel, jellel (ami nekünk kevés, de egy majomnak sok). Így a könyv összesen 10000 betűt vagy jelet tartalmaz. A majom számára közömbös, hogy mit írt le előzőleg, ezért is az örökifjú tulajdonság, az eloszlás geometriai. Az írógép -a latin ábécé 27 betűs- betűinek és jeleinek száma legyen összesen 30. Minden 10000 hosszú mintázat valószínűsége egyenlő az örökifjú tulajdonságnak megfelelően, azaz 29 x 30-10000, de hogy hol jelenik meg egy végtelen hosszú sorozatban, arról semmit nem tudunk állítani, feltehetően sokára, és egy valószínűséggel, majdnem biztosan (az egy valószínűségű esemény nem biztos esemény, csak "majdnem biztos").
Kétdimenziós eset-ben a véletlen számok ábrázolása b függvényében, több dimenziós általánosítás is lehetséges. A képek generálása véletlen számok sorokba tördelésével, ábrázolásával történik, vagy minden képponthoz, pixelhez véletlen színgenerátorral rendelnek egy szint. Jó minőségű véletlen számok ábrázolásai megkülönböztethetetlenül hasonlítanak egymásra. Két különböző véletlen szám ábrázolását a koordinátákon nem sikerült találni.
b =2 esetben: