A számtani és mértani középértékek ábrázolása
(2025 augusztus)
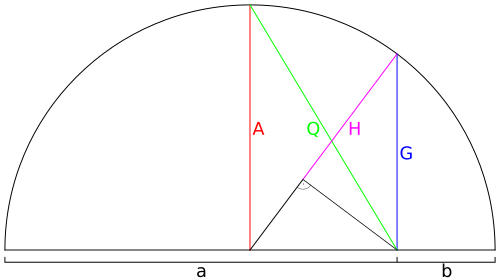
Két szám, a és b középértékei: a H harmonikus közép lilával, a Q négyzetes közép zölddel, a G mértani közép kékkel, az A számtani közép, vörössel
Mivel az átfogó mindig hosszabb, mint a derékszögű háromszög befogója, a diagram mutatja a Q > A > G > H egyenlőtlenséget is.
(https://sv.wikipedia.org/wiki/Fil:Mean-values.svg, https://hu.wikipedia.org/wiki/Harmonikus_k%C3%B6z%C3%A9p)
Várható érték, számtani közép (A): a várható érték becslése a számtani közép, azaz a tényezők, azaz a valószínűségi változók összege osztva a tényezők számával. A valószínűségszámításban a véletlen jelenségek átlagos eredményét írja le. A tényezők valószínűségeivel súlyozott összeggel egyenlő. A számtani középben a két adatsor közül nagyobb súlyt kapnak a kisebb adatok; a harmonikus közép minden adatot ugyanolyan súllyal tekint.
Harmonikus középérték (H): Véges sok pozitív szám harmonikus közepe a tényezők reciprokaiból számított számtani közép reciproka. Több szám harmonikus közepe a kisebb számokat jobban figyelembe veszi; a nagy számok hatása csökken a számtani középhez viszonyítva. Az elnevezés a harmonikus sorból származik (az egész számok reciprokai: a másodiktól kezdve minden tag a két szomszédjának harmonikus közepe). Pl.: A harmonikus közepértéket a fizikában többek között átlagsebesség kiszámítására használjuk, ha az adott sebességekkel egyenlő utakat tettünk meg. A harmonikus közepet pénzügyben az arányok átlagolásához használják.
Mértani közép (G): a két tényező szorzatából vont négyzetgyök. A négyzete, G2 = A x H, azaz a mértani közép négyzete = a számtani közép szorozva a harmonikus középpel. Több tényező mértani közepe: a tényezők szorzatából vont annyiadik gyök, ahány tényező van.
A négyzetes várható érték: (Q) becslése a tényezők négyzetösszege osztva a tényezők számával. Hasznos, ha a változó értékei pozitívak és negatívak is lehetnek, például hullámok esetén (https://hu.wikipedia.org/wiki/N%C3%A9gyzetes_k%C3%B6z%C3%A9p). A négyzetes közép geometriai jelentése: oldalméreteikkel adott négyzetekből az átlagos területű négyzet oldalának kiszámítása.
Medián: egy rendezett adatsorban a középső elem, amelynél az adatok 50%-a kisebb, 50%-a pedig nagyobb értékű. Míg a várható érték (számtani közép, vagy a valószínűségekkel súlyozott átlag) a tényezők átlagértéke és a középső elem között a fő különbség a kilógó értékekkel szembeni érzékenység. A medián kevésbé érzékeny a torzító, kilógó adatokra, ezért a medián alkalmasabb nem normális eloszlások, pl. jövedelmi adatok jellemzésére (https://hu.wikipedia.org/wiki/Harmonikus_k%C3%B6z%C3%A9p).
A kvantilisek a statisztikában a középértékek melletti eloszlás-mutatók. Legyen 0 < q < 1. Ha a rangsorba rendezett sokaságot egy X ismérvérték q : (1 - q) arányban osztja ketté, akkor ezt az ismérvértéket q-ad rendű vagy q-adik kvantilisnek nevezzük. A gyakran előforduló kvantilisek elnevezései:
Tercilisek (a sokaságot három részre osztják),
Kvartilisek (a sokaságot négy részre osztják),
Kvintilisek (a sokaságot öt részre osztják),
Decilisek (a sokaságot tíz részre osztják),
Percentilisek (a sokaságot száz részre osztják).
Kvartilisek (a sokaságot négy részre osztják),
Kvintilisek (a sokaságot öt részre osztják),
Decilisek (a sokaságot tíz részre osztják),
Percentilisek (a sokaságot száz részre osztják).
