Az MI mennyire gyorsítja a világ változását?
(2025 október)
A Mesterséges Intelligencia exponenciálisan, logisztikai görbe szerint gyorsítja a világunk változását az idő függvényében!@ (És ma még gyorsuló szakaszban van, a 30-as években fog tetőzni.) Az adatáramlás exponenciálisan növekvő mennyisége, és az adatáramlás sebessége is, gyorsító hatású.
Az MI gyorsabban változtatja meg a világot, mint az elképzelhető volt, és amibe bele kell születni. Átalakította a munkaerőpiacot, különösen a szellemi munkakörök és a menedzsment terén. Az oktatási rendszer is kihívásokkal nézett szembe a technológia gyors beáramlása miatt, az MI használata elengedhetetlen a jövő generációi számára, nem lett csalás a használata, hanem munkaeszköz, oktatási eszköz lett. „Az internet csak egy enyhe szellő volt ahhoz képest, amilyen hatalmas vihar vár még ránk az MI-vel. A Big Data, a statisztikák készítése, a robotika és az IoT, a generatív MI, a soknyelvű szöveggenerátor ChatGPT és az MI képgenerátorok kapják a legtöbb figyelmet". (Az IoT, Internet of Things, magyarul Dolgok Internete, az elektronikus eszközök és a fizikai tárgyak olyan hálózata, amelyeket szenzorokkal, szoftverekkel és egyéb technológiákkal szereltek fel az adatok interneten keresztüli cseréjére további eszközökkel és rendszerekkel, ezáltal pedig „okossá” téve azokat. Az IoT az okosotthonoktól az iparágakig sok alkalmazást foglal magában, lehetővé téve az adatok gyűjtését, elemzését, előrejelzését és automatizált döntések meghozatalát, ami fokozza a hatékonyságot és a biztonságot.) Az MI nélkülözhetetlen eszköz lett az erőforrások, ellátási láncok optimalizálásában, környezetvédelemben, energiahatékonyságban. A gépek feladata az adatok feldolgozása, a lehetséges döntések javaslata, az embereké a kérdezés, az értelmezés és a döntés. Ami a fizikai másolásban a 3D nyomtatás, az lesz a jelenségek vizsgálatában a szimuláció** az MI-vel.

Van az MI-nek egy képessége, amit ma még alig használunk, ez a hang alapú kommunikáció, ami a fiatalok között gyorsan népszerű lesz, és nincs különösebb eszközigénye. A szükséges szoftver, illesztő program beszédfelismerő része nyelvenként tanításigényes, gépi szempontból egyszerű lenne, de komoly hibaforrás lehet, a pontatlan szóhasználat, kiejtés. A fiataloknál a szövegszerkesztők nélküli kommunikáció miatt lesz népszerű, érdekes lesz látni egy gyereket, amit látszólag telefonál és hadonászik a táblagépe előtt, azaz "legyintésekkel" közöl utasításokat, és számtalan mini appot hív meg szóban, de a jelszóhasználat hangalapú változatait még ki kell találni.
Munkahelyek: Az alsó 90 százalékot, különösen a jövedelem vagy képzettség szempontjából, és a világ hátrányos 50 százalékát is súlyosan érinti majd a munkahelyekről való kiszorulás. A mai mesterséges intelligencia két jelentős szempontból „haszontalan”: nincs kreativitása, és nem képes együttérzésre vagy szeretetre, „egy eszköz, interface, agent az emberi kreativitás felerősítésére”. Az ismétlődő vagy rutinfeladatokkal járó munkakörökben dolgozóknak új készségeket kell elsajátítaniuk, hogy ne maradjanak le. Előfeltétele annak, hogy a mesterséges intelligencia sok területen sikeres legyen, hogy óriási összegeket fektessünk bele az oktatásba, hogy az embereket átképezzük az új munkahelyek ellátására, a munkavállalóknak úgy kell megtanulniuk a programozást, mintha egy új nyelvet tanulnának, vizsgával. Az MI jól kódol, ha valaki ír számára egy supervisort. A távmunka gyorsan terjed, különösen az alkalmas nők körében. A felsőoktatásban a gyorsulás filozófiája (=accelerationizmus) a technológia és az innováció gyors bevezetését szorgalmazza az oktatási rendszerekben, különösen a felsőoktatás, de a középszintű oktatás átalakításában. Az oktatásnak a problémamegoldásra, a lehetséges magyarázatok keresésére, az érvelési képesség fejlesztésére kell koncentrálnia. Az egyetemek online platformokat, mesterséges intelligencián alapuló oktatásokat alkalmaznak, hogy felkészítsék a hallgatókat a globalizált, technológia vezérelt jövőre. A módszerek a kreativitást és a multiszenzoros interakciót használják majd a mélyebb megértés elősegítése érdekében. Akadémiai gyorsítás tehetséges tanulók számára úgy, hogy a doktori képzés az MS képzés közvetlen folytatása, a tehetségesebb tanulóknál évfolyam-kihagyással, vagy két MS képzéssel párhuzamosan. De lesz egy terület, ahol az MI nem lesz nyerő, ez az érveléstan, a szónoklattan, a szónoki érvelés területe.*
A problémafelvetés, jó kérdések megfogalmazása és a válasz értelmezése a lexikális ismeretek mellett is inkább intellektuális felkészültséget kíván meg. Az intellektuális felkészültség értelmi képességet, a tudatot, tudatost jelent, magába foglalja az észlelés, az emlékezés, a gondolkodás, általánosítás, az elvonatkoztatás, az érvelés, eszközkeresés, készítés és a döntéshozatal képességeit. A (cél-) tudatosság (és a humor) a legmagasabb szintű mentális tevékenységek, emberi tulajdonságok. Az intellektuálisan fejlett embereket az új problémák felismerése és megfogalmazása jellemzi, jól, jókor és jót kérdezni kevesek képessége, és nehezebb mint megválaszolni. A jó kérdezést az AI használatával napjainkban is tanuljuk.

Mit tehetünk a lassításért? Az MIés az automatizálás gyorsabban alakítja át az iparágakat, mint ahogy a szabályozások lépést tudnak tartani. Kialakult a fenntarthatóságért folytatott verseny, ami kikényszeríti az innovációt, az MI alkalmazását, megemeli az energiárakat is (persze elsősorban a háborúk). A társadalmi normák és értékek gyorsan változnak, és nem jó irányban, amit a lokális-globális összekapcsoltság és a generációs változások is táplálnak. A félretájékoztatás olyan gyorsan terjed, mint az influenza, kihívást jelentve a felismerési és alkalmazkodási képességünkre. A gazdasági ciklusok rövidülnek, ami korábban évtizedekig tartott, az most évek vagy hónapok alatt bontakozik ki. Magyarországnak egy nem nagy, mindentudó AI-ra, hanem sok kis MI rendszerre van szüksége, mert az MI tanítása túl nagy adatmennyiséget (azaz nagy architektúrát és sok energiát!) igényel. A kis országok lehetőségei korlátozottak nagy generatív MI-k építésében: az egyik legnagyobb generatív chatbot, a ChatGPT például magyar nyelven csak a Wikipédia magyar részéből kapott képzést, ami 128 millió szócikket jelent, míg a Wikipédia angol nyelvű szövegében 80 milliárd szócikk található. Így magyar nyelvű kommunikáció esetén más mélységű és kidolgozottságú válaszok születnek, mert egy alkalmazás csak annyira lehet pontos és helyes, amennyi alapanyagból tud dolgozni. Aki használja, az gyenge magyar válasz esetén, kérdez angolul is. De a Microsoft vállalta, hogy a Copilot számára saját forrásból létrehoz egy legalább 10 milliárd magyar szót tartalmazó adatbázist, amelyet ingyenesen, nyílt forráskóddal bárkinek a rendelkezésére bocsát, aki generatív MI alkalmazást fejleszt. „A Microsoft-ügyben hozott döntés jó példa arra, hogy a GVH versenyjogi eszközökkel tudja segíteni a magyar nyelv érvényesülését a mesterséges intelligencia korában is” . (Nem kell félni, a Google is vállalni fogja a Gemininél, a keresőgépükben már az MI válaszol első helyen.)

Várakozás az ihletre (festmény, Artemisia Gentileschi: A retorika allegóriája, 1650 körül,
*Retorika: A római kori szónoklattan legjelentősebb műve Quintilianus Institutio oratoria (Szónoklattan, szerzője: Marcus Fabius Quintilianus), egy 12 kötetes retorikai tankönyv, amely az ideális szónok felkészítését tárgyalja. Művében a szónokláshoz szükséges készségeket öt fő terület-re osztja: érvek kidolgozása (inventio), elrendezése (dispositio), stílus (elocutio), memorizálás (memoria), és előadás (pronuntiatio).(https://hu.wikipedia.org/wiki/Sz%C3%B3noklattan)
A mű célja hivatásos szónokká nevelni az embereket, a retorikai képességek fejlesztésével. Felépítése: 12 kötetet foglal magában, amelyek a teljes felkészülési folyamatot lefedik. A mű öt kulcsfontosságú szakaszt dolgoz ki a szónoki felkészüléshez:
Inventio (érvelés,találékonyság): Az érvek és mondanivaló kidolgozása.
Dispositio (elrendezés): Az érvek logikus sorrendbe állítása és a beszéd szerkezetének felépítése.
Elocutio (nyelvi stílus): A megfelelő stílus, szavak és képek kiválasztása a meggyőzéshez.
Memoria (emlékezet): A beszéd szövegének megjegyzése és fejből való felidézése.
Pronuntiatio (előadás): A beszéd érzelmekkel és hatásosan történő elmondása.
A szónoklattan, ékesszólástan vagy retorika a szónoklat tudománya, eredetileg díszes külsőségek között előadott beszédeket, ékes stílusú, nyilvános megszólalásokat jelentett. Később a prózai írásművek elmélete volt. Iskolai tantárgy volt a beszéd- és értelmezésgyakorlat mellett. Ma a rendszeres gondolkodás és önkifejezés eszköze, a kulturált érvelés, vitatkozás tudománya. Tárgya minden nyilvános, közéleti megszólalás, minden közéleti kommunikációs helyzet, és szereplője minden nyilvánosan megszólaló ember. Társtudománya a szövegtannak, amely a sikeres közlés, a meggyőző beszéd szempontjai alapján tekinti át a szöveg (beszéd) létrehozását. A klasszikus retorikai elmélet meghatározta a retorika alapelveit, szabályait, eszközeit, amelyek alkalmazhatóak a mindennapi kommunikációs folyamatokban is, kiegészülve a modern nyelvészeti, kommunikációelméleti, pszichológiai stb. ismeretekkel.
**Szimuláció: A szimuláció szó jelentése utánzat, modellezés, imitáció, ma már a virtuális valóság, videójátékok is, azaz olyan vizsgálat, melynél egy rendszer, egy folyamat, gyakran egyszerűsített másolatán, régen fizikai, u.n. deszkamodellen, ma a számítógépes modelljén figyeljük meg, tanulmányozzuk a rendszer viselkedését, tulajdonságait. A szimulációval a folyamat matematikai modell működése alapján rekonstruáljuk a jelenséget. A szimuláció a fizikai vagy a társadalmi folyamat vizsgált elemeit elvonatkoztatja, a valóságot absztrahálja, lényegkiemeléssel leegyszerűsíti. A szimulált valóságot ma már számítógépek segítségével vizsgáljuk, állítjuk elő, az analóg modelleket is digitálisan tanulmányozzuk. Például a repülőgép vagy gépkocsi működését szolgáló épített szimulátor-ok alkalmasak a vezetői tevékenység begyakoroltatására, de történelmi, társadalmi szituációk lényeges adatait is vizsgálhatjuk. A modell lehet fizikai, ekkor a mérete gyakran kisebb, mint az eredeti szerkezet (például vízépítési műtárgyak vizsgálatánál), vagy matematikai (például meteorológia esetén).
A modellezés és a szimuláció alapelvét már James Clark Maxwell (1831-1879) megfogalmazta: „Megfigyelhető, hogy két különböző tudományban a változók olyan rendszere létezik, amelyek között a matematikai kapcsolat ugyanaz, tekintet nélkül arra, hogy a folyamatok fizikai lényege egészen különböző.” A megismerés egyik alapelve Szent-Györgyi Albert-től: „A diák csak akkor tud megérteni egy új fogalmat, egy új jelenséget, ha hasonlítani tudja valamilyen általa már ismert fogalomhoz, jelenséghez, és azt is megérti, hogy az »új« miben különbözik a már ismert »régi«-től.” A matematikai modellezés valós rendszerek és folyamatok leírása matematikai eszközökkel, amelynek során a valóságot matematikai egyenletek, összefüggések vagy más matematikai fogalmakkal képezzük le, hogy megértsük, elemezzük és előrejelezzük viselkedésüket.
Becslési, előrejelzési módszerek:
Trend-becslés***
Bayes-becslés (sok info)
Kálmán-szűrő (Optimális legkisebb négyzetes becslés teljes infóval, már van kevés infós vátozata is)
Maximum Likelihood becslés (MLH), rekurzív változatok (kevés info)
Legkisebb négyzetes hibájú becslés (LMS), rekurzív változatok, (kevés info).
Példa a kevés infós rekurzív becslésekre: Θn,i = Θn-1,i + 1/n (yn - yn,mért) (Σi gi2)-1/2 gn , ahol Θn az n -ik lépésben becsült paramétervektor, és i = 1,2,...,dimΘ, és yn = ΘnT gn az n-ik lépésben becsült output előrejelzés, és gn = δyn /δΘn gradiensvektor, mért értékeket tartalmaz (https://bencsik.rs3.hu/a-sarki-jeg-a-2020-as-evekben/68-a-sztochasztikus-approximacio-konvergenciajarol.html), lineáris esetben, az esetek ≈ 95%-ában egyszerűen számítható.
Diszkrét események szimulációja és az MI elterjedésével a számítógépeken már a bonyolult rendszerek is vizsgálhatóak, a véletlen hatásokat additív véletlen számokkal, zajokkal modellezzük. A matematikai modellekben differenciálegyenletek, algebrai egyenletek, táblázatosan összerendelt értékek, sztochasztikus összefüggések stb. írják le a valóságban lezajló folyamatokat. Szűkebb értelemben a szimuláció a matematikai modell futtatása kisérlettervezéssel kapott bemenő és kezdőértékekkel. A modellezés első lépése az adatgyűjtés, utolsó lépése a validálás.
A szimulációs célok lehetnek: törvény-, szabályszerűségek felismerése, előrejelzés, modellek ellenőrzése, hitelesítése, vezérlés, irányítás, döntés-előkészítés, működés, paraméterérzékenység vizsgálata. A szimuláció módszertana a lehetséges vizsgálatokkal (mérés, kísérlet, gondolatkísérlet, hipotézisvizsgálat,...), a modellek osztályozásával, a mintavétel szabályaival; típusmodellek készítésével, használatával; kísérlettervezéssel, értékeléssel, validálással foglalkozik.
Egy, a mérnöki gyakorlatban használt alkalmas validálási mérték a becsült és megfigyelt folyamatok szórásnégyzeteinek, szórásainak aránya, és az arány idősorok és sokaságok esetén is bizonyíthatóan alkalmas műszaki mérték. A „szigmás” állítások a fizika és a tudományos kutatás világában a statisztikai bizonytalanság-bizonyosság kifejezésére szolgálnak. A „szigma” (σ) a matematikai statisztikában a szórás jelölésére használt jelölés, amely megmutatja, mennyire térnek el az adatok az átlagtól. Ha egy fizikus azt állítja, hogy egy mérési eredmény „5 szigmás”, az azt jelenti, hogy az érték igen valószínűen nem véletlen zaj eredménye. A nagyobb szigma-értékek növelik a megbízhatóságot: például a Higgs-bozon felfedezését a fizikusok csak akkor jelentették be hivatalosan, amikor az eredmények elérték az 5-szigmás szintet, ami azt jelenti, hogy a véletlen előfordulás esélye rendkívül kicsi (kb. 1 a 3,5 millióhoz) volt. A tudományos állításokban a valószínűséget határozzák meg numerikus skálán, amely segít eldönteni, hogy egy jelenség valódi felfedezés, vagy puszta véletlen (8*).
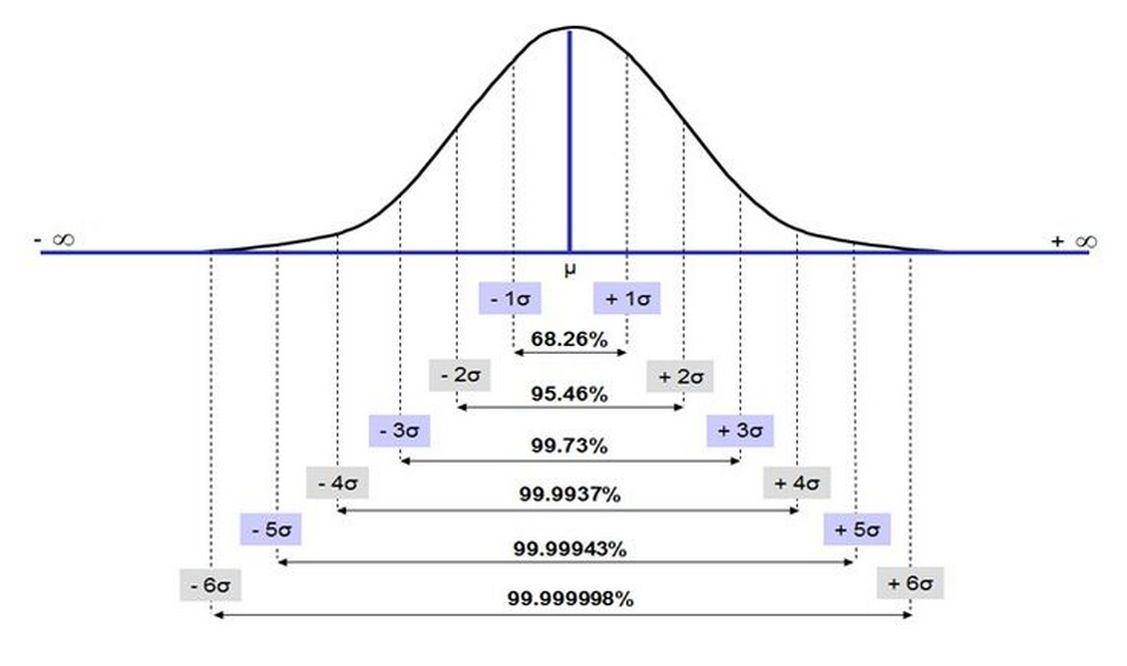
Szórásintervallumok valószínűségei normális eloszlás esetén, a 3σ -ás intervallum a gyakori
@
***Még nem értük el az inflexiós pontot, ami a 30-as években lesz.
Az egyszerű trendbecslő módszerek lineáris, exponenciális, logisztikus görbék paramétereit számítják regresszióval. A logisztikus trendfüggvények olyan növekedési modellek, amelyek a növekedés lassulását és egy felső korlát elérését írják le, gyakran inflexiós ponttal jellemezve, és magukban foglalják a Verhulst-féle, a Pearl–Reed-féle és a Gompertz-függvényt is. Ezek a függvények széles körben alkalmazhatók, például népességnövekedés, technológiai diffúzió vagy fertőző betegségek terjedésének modellezésére, ahol kezdetben gyors növekedés, majd egyre lassuló növekedés figyelhető meg, míg végül stabilizálódik a folyamat. A logisztikus trendfüggvények matematikai modellek, amelyek egy adott populációban, erőforrásban vagy jelenségben a kezdetben gyors, majd lassuló, végül pedig telített növekedést írják le, jellegzetességük az inflexiós pont, ahol egy egyenes érintő metszi a görbét.
gy egy jelenléte, ami azt jelenti, hogy a növekedés sebessége a telítettségi szint felé közeledve a maximumról csökken.
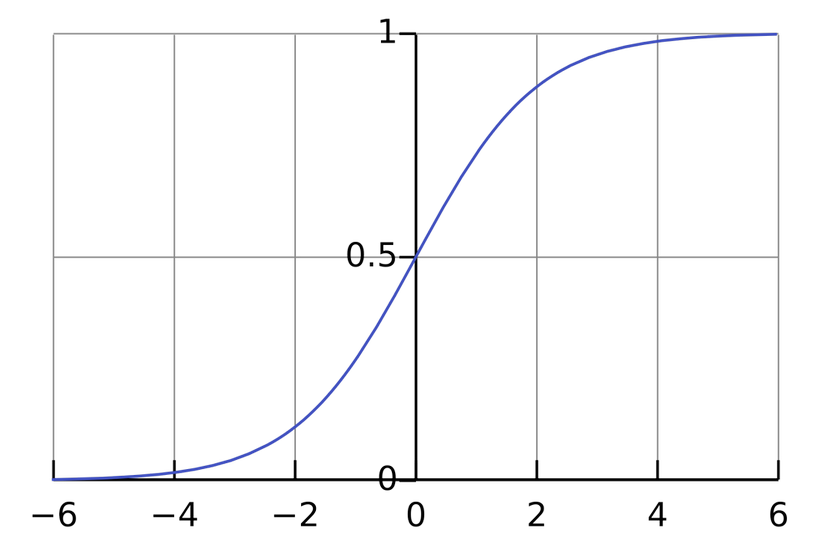
A várható növekedés gyakran logisztikai görbét (https://en.wikipedia.org/wiki/Logistic_function) követ, mint a folyamatok általában a természetben. Számos természeti folyamat úgy zajlik le, hogy az időben, egy kezdeti értéktől gyorsulva indul, majd lassulva közeledik a végső állapotig.
Logisztikus görbe, az origó felett van az inflexiós pont-ja
A logisztikus görbe egyenlete igen egyszerű: 1/( 1 + exp (-kt) ), ahol t = 2,4,6,... A függőleges tengelyen a szintemelkedés a maximummal normált értéke olvasható le, és k egy illesztő paraméter. A görbe alatti terület igen egyszerűen számítható kt függvényében: ln ( 1 + exp(kt) ). Nehezebb kérdés a maximum és k becslése, számítása, azaz a skálázás. A nevezetesebb logisztikai görbék több paramétert használnak.
A Markov-egyenlőtlenség élessége általánosan nem függ a viszonyítási paraméter megválasztásától. A Markov-egyenlőtlenség változatai:
Az egyenlőtlenség annak a valószínűsége, hogy egy X valószínűségi változó értéke nagyobb mint egy megadott ε küszöbérték. Két normális
(vagy egyenletes) eloszlás összehasonlításánál az ε viszonyítási paraméter alkalmas megválasztása a Markov egyenlőtlenségekben alkalmas
eszköz lehet az információ tartalom értékelésére.
Ha X ≥ 0 valós valószínűségi változó, E(X) várható értéket jelöl, akkor ε > 0 esetén:
P {X ≥ ε } ≤ E [X] / ε .
I. Egy további változatot kapunk, ha az ε paraméter helyére az ε D[X] mennyiséget, a szórás ε-szorosát helyettesítjük (azaz ε D[X] → ε, vagy az X/D[X] relatív változó helyettesítésével): P {X ≥ ε D [X] } ≤ E [X] / ε D [X]. Az E [X]/D [X] relatív várható érték arányos az eloszlás várható érték körüli információtartalmával (csúcsosságával), ezért kisebb szórású valószínűségi változókra nagyobb valószínűséget, és kisebb εD [X] küszöb értéket kapunk. A relatív várható értékre vonatkozó változat átírható az alábbi alakba:
P {X/D [X] ≥ ε } ≤ E [X] / ε D [X] . Az Y = X/D [X] változóra igaz, hogy D [Y] = 1.
III. Tekintsuk az X → helyettesítést, amikor a Csebisev-egyenlőtlenséget kapjuk, és a Var (X) = D 2(X) jelöléssel egy a konstanssal:
helyettesítést, amikor a Csebisev-egyenlőtlenséget kapjuk, és a Var (X) = D 2(X) jelöléssel egy a konstanssal:

IV. Továbbá a λ2 Var (X) → a2 helyettesítéssel kapjuk, hogy P { abs (X - E(X)) ≥ λ D(X) } ≤ 1 /λ2, azaz P { Z ≥ λ } ≤ 1/λ2 , ahol Z standardizált véletlen változót jelöl.
| k | Min. % within k standard
deviations of mean | Max. % beyond k standard
deviations from mean |
|---|
| 1 |
0% |
100% |
| √2 |
50% |
50% |
| 1.5 |
55.56% |
44.44% |
| 2 |
75% |
25% |
| 2√2 |
87.5% |
12.5% |
| 3 |
88.8889% |
11.1111% |
| 4 |
93.75% |
6.25% |
| 5 |
96% |
4% |
| 6 |
97.2222% |
2.7778% |
| 7 |
97.9592% |
2.0408% |
| 8 |
98.4375% |
1.5625% |
| 9 |
98.7654% |
1.2346% |
| 10 |
99% |
1% |
V. A Cantelli egyenlőtlenség élesebb mint az eddigi egynlőtlenségek: (https://en.wikipedia.org/wiki/Cantelli%27s_inequality ) ![{\displaystyle \Pr(X-\mathbb {E} [X]\geq \lambda )\leq {\frac {\sigma ^{2}}{\sigma ^{2}+\lambda ^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fd73c057659174a53a933f0330415148ecf7bd6) vagy λσ→ λ helyettesítéssel kapjuk, hogy P { Z ≥ λ } ≤ 1/ (1 + λ2), a standardizált változóra érvényes alakot.
vagy λσ→ λ helyettesítéssel kapjuk, hogy P { Z ≥ λ } ≤ 1/ (1 + λ2), a standardizált változóra érvényes alakot.
A Cantelli-egyenlőtlenségben a D 2 (z2) → λ 2 helyettesítéssel kapjuk a P { Z ≥ D [ Z2] } ≤ 1/κ alakot, ahol κ = D 2 (Z2) + 1, a lapultság standardizált változók esetén. Az egyenlőtlenség a nulla várható értékű korrelálatlan zaj folyamatok vizsgálatakor lehet hasznos. A szimmetrikus eloszlások páratlan rendű centrális momentumai nullák, mivel az összegben a várható értéknél kisebb értékekből számított tagok és a várható értéknél nagyobb értékekből számított tagok kiejtik egymást.
Normális és az egyenletes eloszlások - melyek a várható érték körül szimmetrikus sűrűségfüggvényű abszolút folytonos eloszlások- összevetése: az N (M(η), D2 (η)) normális eloszlás esetén az η valószínűségi változó 0.99730 valószínűséggel esik az M(η) várható érték 3 D (η) szélességű környezetébe, ekkor a terjedelme T = 6 D (η) (Prékopa, i.m. 224.o.). Annak az egyenletes eloszlású valószínűségi változónak, amelyiknek a várható értéke M(η) és a terjedelme T = 6 D (η) értékű, a szórásnégyzete T2/12 = 3 D2 (η), azaz egyenletes U(M(η), 3 D2 (η)) eloszlású: a szórásnégyzete háromszorosa a normális eloszlás szórásnégyzetének. M(η) és D (η) csak a normális esetben független valószínűségi változók: egy fontos gyakorlati esetben, amikor M(η) = 0, akkor az egyenletes eloszlás szórásnégyzete független, ami a Kálmán-szűrő esetén fontos állítás.
A függetlenség: az elemi események halmaza páronként független, ha két esemény együttes bekövetkezésének valószínűsége a két esemény valószínűségeinek szorzata. Egy másik meghatározás: ha egy esemény feltételes valószínűsége az esemény valószínűségével egyenlő, ellenkező esetben az esemény feltételes várható értékére vonatkozóan ld. a Kálmán-szűrőt (https://en.wikipedia.org/wiki/Kalman_filter), a Bayes-becslést.
A nem együttesen bekövetkező, egymás utáni események sorozatot alkotnak. Sorozatok esetén az elemi események ismétlődnek, ekkor a függetlenség definíciója a sorozatok elemeire: ha egy új elem csak a legutolsó elemtől függ és az előző elemektől független, akkor sorozat Markov folyamat. Amennyiben az új elem az utolsó elemtől -és megelőző elemektől is- független, akkor sorozatot örökifjú sorozatnak (https://hu.wikipedia.org/wiki/%C3%96r%C3%B6kifj%C3%BA_tulajdons%C3%A1g) nevezzük. Bizonyított, hogy az utóbbi esetben a sorozat diszkrét esetben geometriai eloszlású, folytonos esetben pedig exponenciális eloszlású.







![{\displaystyle \Pr(X-\mathbb {E} [X]\geq \lambda )\leq {\frac {\sigma ^{2}}{\sigma ^{2}+\lambda ^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fd73c057659174a53a933f0330415148ecf7bd6)