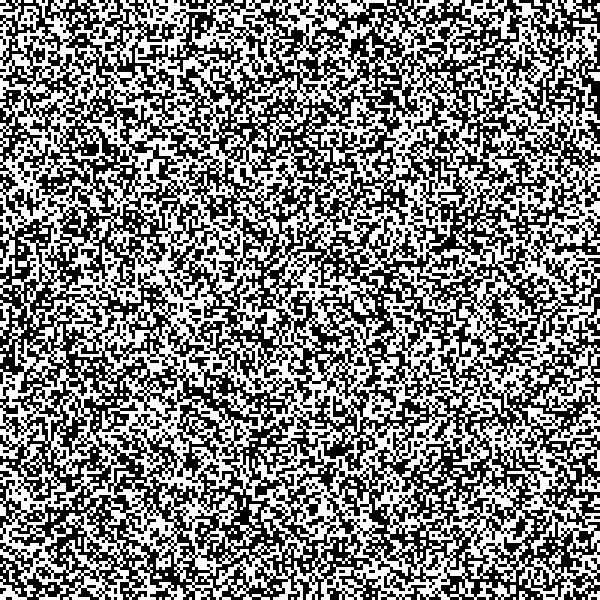A NEW CHAPTER OF THE CHAOS THEORY: CHAOTIC SYSTEMS

 

 

 

 

 

 THE CHAOS THEORY:

 

 

CHAOTIC SYSTEMS

 

 

 

 

 

(April 2025)

 

 

 

ABSTRACT

The labil systems in chaos theory are only partially deterministic because after a while their behaviour becomes independent of initial states. The unpredictable i.e. chaotic behaviour is an immanent property of systems, which can only be described by probabilistic and stochastic means. There are also systems that are unpredictable e.g. in random walk problems, random numbers, random graphs. The description of unpredictable systems is done using the concepts of independence and memorylessness. For unpredictable systems the distributions suitable for their description are normal, uniform, geometric and exponential distributions. For normal and uniform distributions, the expected value and the variance squared are independent quantities, for the uniform distributions they are only conditionally independent quantities, when the expecteded value equal to zero while geometric, exponential and Poisson distributions are memoryless distributions, i.e. the future of the process is independent of the present and the past of the process. At Markov processes the future of the process depends only on the present. The memorylessness property distinguishes systems describable by exponential, Poisson and geometric distributions as completely chaotic systems from systems describable by other distributions.

 

 

 

Chaos theory (https://en.wikipedia.org/wiki/Chaos_theory) is concerned with nonlinear deterministic time-dependent labil systems whose behaviour can only be partially predicted, despite deterministic regularities, and after a finite period of time their behaviour becomes independent of initial states. The systems considered are sensitive to initial conditions, also known as the butterfly effect.
Even simple deterministic systems that can be described by a few state variables can exhibit complex, unpredictable behaviour. The deterministic systems considered in chaos theory can be described partly by statistical stochastic methods, not because they are complex, but because chaotic behaviour is an intrinsic (immanent) property of the systems, and after a finite time their behaviour becomes independent of initial conditions. For real deterministic systems, asymptotic behaviour is clearly determined at t = infinity, so only partially deterministic systems can behave chaotically.
For example, the motion of a double pendulum is independent of its initial state after a finite period of time.

 

 

                                                                            (https://scienceworld.wolfram.com/physics/DoublePendulum.html)

 

A double pendulum is a simple physical system consisting of two pendulums attached to each other, whose chaotic motion is initially governed by deterministic differential equations, but after a while its motion becomes random and chaotic. There are several variants, the length and mass of the two pendulums can be the same or different(https://scienceworld.wolfram.com/physics/DoublePendulum.html). The description of the motion can be either 3-dimensional or 2-dimensional.

 

 

 

                                                                                                                                                              

                                                                                      (https://scienceworld.wolfram.com/physics/DoublePendulum.html)

 

The considered systems with chaotic behaviour are only partially deterministic systems, in contrast to the meaning of the word chaos means complete randomness (uncorrelated, possibly independent processes). After a finite time, instability, local disorder, characterises the chaotic systems. Behaviour is locally unstable if, starting from two starting positions close to each other, the differences between the states of the system increase in finite time in an unmodelled, unpredictable way. In 1961, the American meteorologist Edward Lorenz used a computer (Royal-McBee LGP-30), now considered very slow, to test his three-degree-of-freedom nonlinear convection model. On one occasion he wanted to recalculate a data series and to save time, he fed the output of an earlier simulation back into the computer. The new result quickly diverged from the last one. He suspected a computer error, but as he discovered, the computer was not at fault. The computer was plotting the data to 6 decimal places, but Lorenz was only writing it back to the machine to 3 decimal places. This small inaccuracy caused the very large discrepancy. In a 1963 paper, Edward Lorenz recognised the high sensitivity of nonlinear deterministic systems to small deviations in initial conditions. The phenomenon is often cited as the butterfly effect, based on the title of one of his lectures, Predictability: Does the flap of a butterfly's wings in Brazil set off a tornado in Texas? Small variations in the initial conditions cause unmodelable large changes in the state of an labile system - a system in an labile equilibrium state - and therefore long-term prediction of its behaviour is impossible, which is a fundamental property of labile systems.

The word chaos was introduced by Tien Yien Li and James A. Yorke in their 1975 article Period three implies chaos... "According to the Japan Foundation for Science and Technology, Yorke received the award for his work in the study of chaotic systems, while Mandelbrot received the award for his work on fractals. Although the Japan Prize is less well known in the public consciousness than the Nobel Prize and the Fields Medal, which are announced and awarded with increased media attention, the prize, which carries a cash award of $412 000, is hardly less recognised in scientific circles than the latter." There is an area of physics called quantum chaos theory, another chapter of chaos theory that deals with non-deterministic systems following the laws of quantum mechanics and another chapter where the behaviour of systems is unpredictable and systems can only be described by statistical, probabilistic methods.

 

CHAOTIC SYSTEMS

Unpredictable processes have independent events, steps. The Wiener process and white noise are the best known. Among the probability distributions, many probability variables from independent experiments are known, but the distributions with the memorylessness property of geometric, exponential and Poisson distributions are suitable for describing unpredictable (= chaotic) systems and processes.

Random walk (https://en.wikipedia.org/wiki/Random_walk) is a stochastic process, often consisting of random steps on integers, starting at 0, and e.g. with equal probability of +1 or -1 step at each step. Other examples are the trajectory of a molecule as it moves through a liquid or gas (Brownian motion), the search path of an animal looking for food, the prices of fluctuating stocks, and the financial situation of a gambler. Many processes can be modelled using random walk models, even if these phenomena are not necessarily random in reality. Given a particle at the origin at time t = 0, the central limit theorem says that after a large number of independent steps of a random walk, the position will be tε/δt away, where t is the elapsed time, ε is the step size, and δt is the time between two consecutive steps.

 

 

 

Random walk in two dimension (https://hu.wikipedia.org/wiki/V%C3%A9letlen_bolyong%C3%A1s)

 

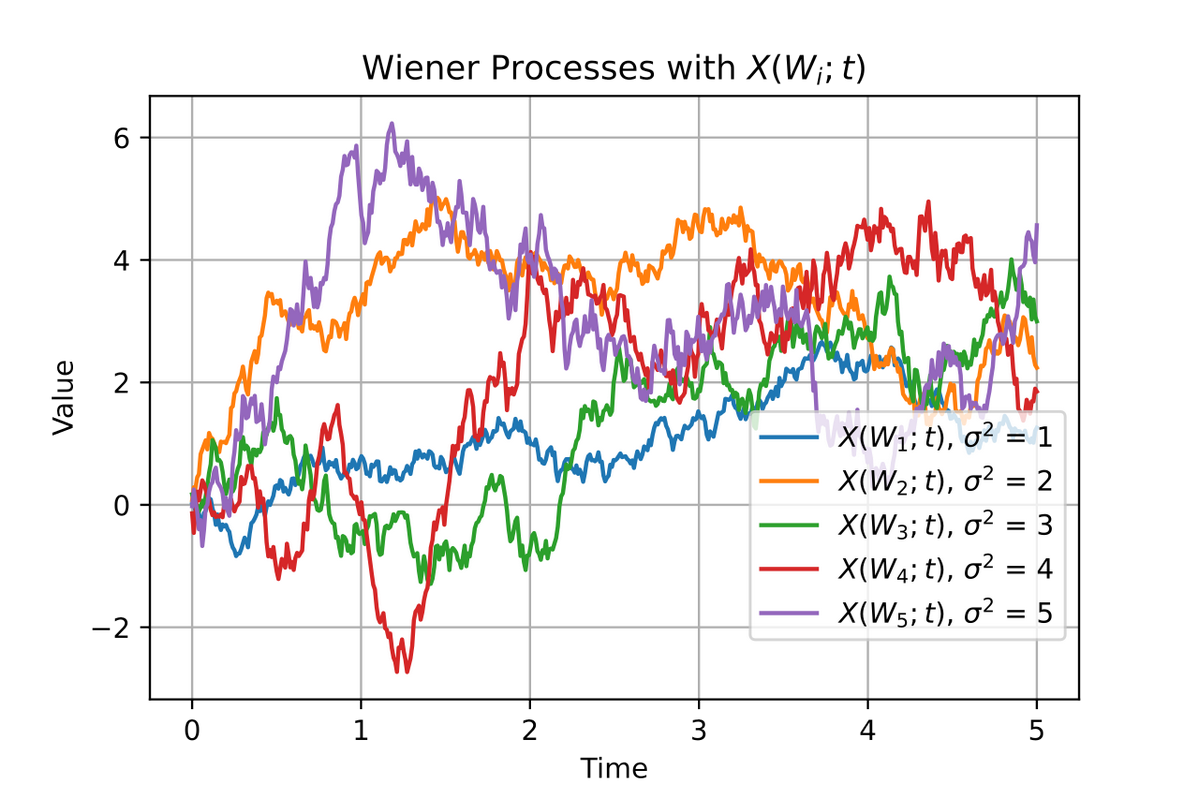
In mathematics, the Wiener process, which is related to wander problems (https://en.wikipedia.org/wiki/Wiener_process), Brownian motion, and the historical physical process of the same name, and is also related to white noise processes. The process is a stochastic process of real-valued, continuous or discrete-time independent increments discovered by Norbert Wiener, where the increments have a normal distribution with zero expected value, and whose derivative process is a white noise process. It is often used in applied mathematics, economics, quantitative finance, evolutionary biology and physics. Properties of the Wiener process _t:

 

1.  
2. ${\displaystyle W}$_t is a process with independent increments, i. e. for every  ${\displaystyle t>0,}$ the increment  ${\displaystyle u\ge 0,}$ is independent their past values. When the process is with independent increments if 0 ≤ s₁ < t₁ ≤ s₂ < t₂ than W_t1 − W_s1 és W_t2 − W_s2 are independent variables. 
3. ${\displaystyle W}$Increments of _t have normal distribution, ${\displaystyle W_{t+u}-W_t\sim \mathcal{N}(0,u).}$ 
4. The process of _t   in continuous case: almost certainly in continuous t.
5. 1. 
   2.                                                                         (https://en.wikipedia.org/wiki/Wiener_process)

 

 

In physics, Brownian motion (https://www.whoi.edu/cms/files/lecture06_21268.pdf) is a continuous, random thermal motion of suspended particles in gases and liquids, discovered by the English botanist Robert Brown when he examined pollen particles mixed with water. The motion was important evidence of the atomic structure of matter. It is a good example of global mixing in chaos theory, whereby, given typical initial conditions, a system will converge to all possible states in a sufficiently long time. The suspended particles undergo constant collisions during their motion, and their behaviour is described by Maxwell's velocity distribution function. Brownian motion trajectories are generally random, continuous and irregular trajectories. Brownian motion is not uncorrelated because the position of a particle at a given instant in time depends on where it was at the previous instant. Brownian motion is a Markov process, which means that a given position of a particle depends only on its position at the previous instant in a random way, and is independent of the positions before it. A characteristic of Brownian motion is that the scattering square increases proportionally with time, so the process is nonstationary, moving away from its initial position proportionally to the square root of time or the number of steps.

White noise (which is a derived process of the Wiener process) is noise whose power density is independent of frequency, i.e. its spectral density is constant over the entire frequency range. The successive noise values are uncorrelated (https://en.wikipedia.org/wiki/White_noise). In reality, there is no infinite bandwidth white noise because it would have infinite power, so we consider band-limited white noise in practice. In numerical simulations, the upper cut-off frequency for sampling is half the sampling frequency. Although the white noise process is uncorrelated, there is a low probability that longer continuous intervals but somewhere can occur with probability 1 in the process, one has not yet seen at band-limited white noise.

 

Uncorrelated, independent processes, conditional independence, Markov processes and the memoryless property
Correlation measures the strength of a linear relationship between two arbitrary values. Uncorrelation does not necessarily mean independence, but it is certain that there is no linear relationship between the values. If the correlation of two random quantities is zero, they are uncorrelated and the relationship is described by conditional probabilities. It is characteristic of normally distributed probability variables that if they are uncorrelated, then they are independent, as well. Thus, correlation is well suited to measuring the strength of the relationship between measurable quantities that are considered to be normally distributed. The uncorrelated probability variables for white noise with zero expected value, i.e. uniformly distributed, are conditionally independent.

Conditional independence is a generalisation of the independence of events, sets of events, probability variables using conditional probability and conditional expected value, and conditional expected value is used to define conditional probability in probability theory (https://en.wikipedia.org/wiki/Conditional_expectation).

The conditional expected value can be a probability variable or a function, calculated by conditional probability distribution, or by projection into the past of a process in realisation theory, for example. If the probability variable can take only a finite number of values, then the “condition” is that the variable can take only a subset of these values. Formally, in the case where the probability variable is defined on a discrete probability space, the ‘conditions’ are partitions of this probability space.
Independence: a set of elementary events is pairwise independent if the probability of two events occurring together is the product of the probabilities of the two events, or by another definition: the conditional probability of an event is equal to the probability of the event. Successive events that do not occur together form a sequence. In a series, the elementary events are repeated, then the definition of independence is: if the occurrence of an event (or elements) depends only on the last event or element and is independent of the previous ones, then it is a Markov process.
If the new element is independent of the last elements -so the preceding elements-, then the series is called a memoryless series. It have been proved that the memoryless series has a geometric distribution in the discrete case, which is the distribution of the series of numbers of discrete white noise with uniform distribution, and has an exponential distribution in the continuous time case.

 

For completely chaotic systems, the distributions that can be used to describe the systems are the normal, uniform, geometric and exponential distributions. For normal distributions, the expected value and the variance squared are independent quantities, and for uniform distributions  the expected value and the variance are conditionally independent quantities iff the expected value is zero, while geometric and exponential, Poisson distributions are memorylessness distributions, i.e. the future of the process is independent of the present and the past of the process.

 

For Markov processes (e. g. the Wiener process) the future of the process depends only on the present. The term Markov process refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history, depending only on only its present. It is named after the Russian mathematician Andrei Markov. In the strong Markov property, the meaning of ‘present’ is sometime defined by a probability variable known as a stopping time. A Markov random field extends the property to two or more dimensions.

 

The exponential distribution is often used to model random time periods, waiting times:
- the hereditary property of the exponential distribution models waiting times well,
- the time it takes to serve one person in a shop (queuing theory),
- the time between two customers arriving at a shop,
- the time it takes to perform a calculation on a computer,
- the theory describing traffic situations,
- the reaction time of one person,
- the time between two events occurring, e.g. for incandescent lamps (reliability theory),
- modelling the spread of an epidemic, the spread of an infection, but also the recovery time,
- the decay time of radioactive particles.

 

A Poisson process (https://en.wikipedia.org/wiki/Poisson_point_process) is a counting process where T1, T2, . . intervals are independent probability variables with exponential distributions. Its basic process is a continuous-time counting process {N(t), t ≥ 0} with the following properties: N(0) = 0, and is characterized by independent increments, stationary increments (the distribution of the number of occurrences in any interval depends only on the length of the intervals) and no simultaneous events. The waiting time for the next event has an exponential distribution. Memoryless i.e. successive arrival events are independent and an event at time t is not affected by any of the events before time t. Applications:
- telephone call arrivals,
- goals scored at football matches,
- requests to web servers.
- particle emission during radioactive decay (which is an inhomogeneous Poisson process),
- queuing theory in which queuing of client-server queues is often a Poisson process.

 

The geometric distribution can be used:
- to analyse waiting times before a given event,
- theory describing traffic situations,
- to determine the lifetime of devices and components,
- to determine waiting times until the first failure,
- to determine the number of frequent events between two independent rare events,
- applications such as testing the reliability of devices,
- insurance mathematics,
- to determine the failure rate of data transmission,
- the geometric distribution is the distribution of independent Bernoulli experiments. A generalisation of the geometric distribution is the binomial distribution over several successful trials, which is expressed in two ways: either it is expected to take rth successful trial, or it is emphasised that rth successful trial took n trials. The geometric distribution is a negative binomial distribution for the parameter r=1.

 

E.g. in queueing theory (https://en.wikipedia.org/wiki/Queueing_theory) the  model is constructed so that queue lengths and waiting time can be predicted. 

Queueing analysis is the probabilistic analysis of waiting lines, and thus the results, also referred to as the operating characteristics, are probabilistic rather than deterministic. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service, and has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company.  These ideas have since seen applications in telecommunications, traffic engineering, computing, project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals. Consider a queue with one server and the following characteristics:

 

• ${\displaystyle \lambda }$: the arrival rate (the reciprocal of the expected time between each customer arriving, e.g. 10 customers per second)
• ${\displaystyle \mu }$: the reciprocal of the mean service time (the expected number of consecutive service completions per the same unit time, e.g. per 30 seconds)
• n: the parameter characterizing the number of customers in the system
• ${\displaystyle P_n}$: the probability of there being n customers in the system in steady state, and analyzis leads to the geometric distribution formula  when     λ / μ < 1. 

In the one dimensional case, we will consider discrete memoryless series, which are geometrically distributed. If the events of a series are uniformly distributed, with probabilities equal to 1/b, if b is the number of the elementary events, b also denotes the base number of the number system, then some arbitrary k (k=1,2,3,...,kmax) long sequence of the independent elementary events has the probability (b-1)/b^k .The parameter of the distribution is (b-1)/b, which is also the probability of a series of unit lengths. The expected value of the distribution is b/(b-1), and the sum of the probabilities has 1 - b^-kmax .
Note: For non-countably infinite sequences, the Haar measure (https://en.wikipedia.org/wiki/Haar_measure) is finite in the binary case, i.e. it is a normalizable measure. Although the computation of the Haar measure is complicated, it is an essential statement that there is a measure in the uncountable binary case (because for uncountably infinite sequences the arithmetic mean and the weight are usually divergent). The main queueing models are the single-server waiting line system and the multiple-server waiting line system. These models can be further differentiated depending on whether service times are constant or undefined, the queue length is finite, the calling population is finite, etc. 

For example, someone's date of birth and random number, in the structure ddmmyy can be retrieved at https://www.piday.org/find-birthday-in-pi/: e.g. 11 January 2011 - the date is '11-11-11', written on the number is in 51150 position in pi, and the number has 9 x10^-6  probability.

Another example: given some pre-recorded text, and a monkey randomly taps the keys of a typewriter indefinitely, it is unlikely that the monkey will eventually write that text, but will do, a mathematical proof of this statement is possible. Cicero argued thus in De natura deorum:
"He who believes this, may also believe that by throwing a bag of twenty-one letters on the ground, the Annales will be read. I doubt if even a short passage of it will appear." Cicero was well aware that the probability of a meaningful text appearing is small, and its possible appearance is inversely proportional to the length of the text. Suppose that the long of the Annales in question is 100 pages long, with 100 letters or signs per page (which is not enough for us, but enough for a monkey). The book contains a total of 10,000 letters or signs. It is indifferent to what it has previously written down for the monkey, since the memoryless property, the distribution is geometric. Let the total number of letters and signs in the typewriter be 30. The probability of each 10,000 long patterns is equal, according to the perpetuity property, i.e. 29 x 30^-10000, but where they appear in the sequence we can say nothing about, presumably at long intervals, and with a probability of one, almost certainly (an event with a probability of one is not a certain event, only "almost certain").

 

In the two-dimensional case of plotting random numbers as a function of b, a multidimensional generalization is possible. The images are generated by serializing random numbers, or by assigning a level to each pixel with a random colour generator. Good quality representations of random numbers are indistinguishably similar. Representations of two different random numbers on the coordinates have not been found. When b =2:

 

 

 

 

                                                                        (https://www.dreamstime.com/illustration/abstract-noice.html)

 

Note that the pattern in two dimensions is a white-black blotch, with mesh-lines in places, and apparently irregular patterns even for higher b values. As the number of pixels increases, there is a small probability that larger black-white patches would appear, corresponding to a decreasing probability that longer sequences would occur in one dimension. Asymptotically, a sample image with the same pixel number can be blacked-out.

If b=3 (white, black, grey)

 

 

 

(https://www.dreamstime.com/illustration/abstract-noice.html)

 

 

If b= 4 (green, yellow, blue, red)

 

 

 

 

 

(https://commons.wikimedia.org/wiki/File:Every_pixel_has_a_random_color.png)

 

b = 5 ((green, yellow, blue, red, white) 

:

 

(https://graphicdesign.stackexchange.com/questions/26174/how-can-i-create-a-random-pixelated-pattern, and https://graphicdesign.stackexchange.com/questions/26174/how-can-i-create-a-random-pixelated-pattern)

 

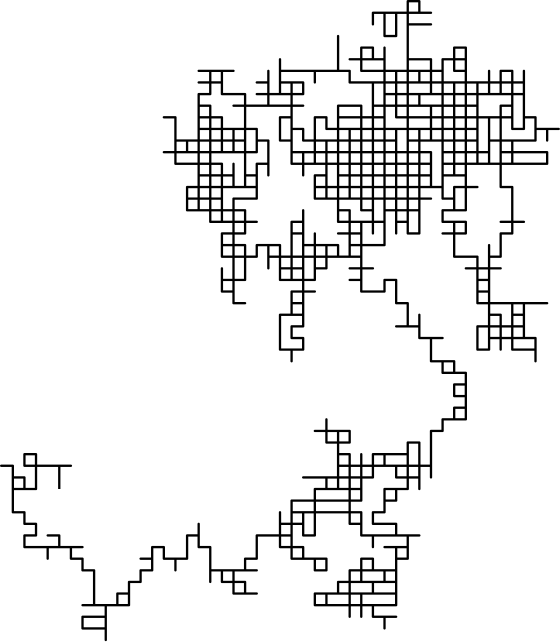
For graphs (https://ematlap.hu/tudomany-tortenet-2020-11/957-mi-is-az-a-perkolacio): percolation (literally leakage) can be interpreted on any finite or infinite graph, and has two basic variants: in edge percolation, the edges of the graph are drawn independently with probability p equal to the probability of being open or closed by 1-p; in vertex percolation, the vertices are drawn as open or closed. In both variants, the basic phenomena are the same. We think of the closed edges as the ones that we have deleted, and the question is from where to go through the remaining open edges, i.e. what are the remaining random graph's connectivity components. A useful study for leakage models of liquids and gases.

 

 

                 Where can be reached from the open edges for square grid and p=0.25, 0.5, 0.75? The longest path is highlighted in red

                                                                (https://ematlap.hu/tudomany-tortenet-2020-11/957-mi-is-az-a-perkolacio)

*

The fact that a process is a non-stationary stochastic process does not imply that it is chaotic and unpredictable. Non-stationary stochastic processes can often be transformed into stationary ones. In the simplest examples, trend components (linear, exponential, logistic, periodic...) can be eliminated by estimation, or, by differentiation, the original process can be transformed into a stationary stochastic process in incremental processes. Nonlinearity can also be well handled by linear estimation if the model is linear in the estimated parameters. The goal of deriving trend components is to eventually describe the system with linear models, ARMA or Kalman filter. For the description of chaotic systems, the methods discussed are inappropriate because chaotic systems are not predictable. In vector space system description, the future of the process is projected onto the present and the past of the process, the projection vector is the estimate, which is a conditional expected value vector perpendicular to which the unpredictable estimation error vector, the distribution of the noise vector being zero expected value Gaussian white noise, or an uniformly distributed white noise.