KURTOSIS → DEFINITION OF PEAKEDNESS

KURTOSIS → DEFINITION OF PEAKEDNESS

(2022)

In probability theory and statistics, kurtosis (flatness, https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis, Greek: κυρτός, kyrtos meaning "curve") is a measure of the "width" of the probability distribution of a real-valued random variable, describing the frequency of data far from the expected value. Flatness describes the weight of the distant data, not the configuration of the data close to the mean. Most often used as a relative fourth moment of κ = μ₄/σ⁴ : the kurtosis is the expected value of the fourth power of the standardised data.

For standardised variables z according to Moors: if z = (x - μ)/σ, where x is a random variable, μ is its expected value and σ is its standard deviation, then flatness κ = E [z⁴] , E denotes expected value, and because for standardised variables σ ⁴ = 1. Then κ = var [ z ²] + [ E [z ^2] ] ² = var [ z ²] + 1.

The reciprocal of var [z ²] + 1 is related to the peakedness: the frequency of data near to the expected value.

If k > 0, then for the standardized variable z, we use the Cantelli (https://en.wikipedia.org/wiki/Cantelli%27s_inequality)

inequality:

$P(Z\geq k)\leq {\frac {1}{1+k^{2}}}.$

holds. We get a new inequality in the form of

P { z ≥ D [ z ²] } ≤ 1/κ,

holds, where κ = μ₄ since k ² + 1 = κ = E[ z ⁴] = var [ z ²] + [ E ( z ²) ] ² = D² [ z²] + 1. (Moors, J. J. A. (1986), "The meaning of kurtosis: Darlington reexamined", The American Statistician, 40 (4): 283-284), and https://en.wikipedia.org/wiki/Kurtosis#Excess_kurtosis) where var [ z²] = E [ z² - E(z²)]² and D [ z ²] denotes the standard deviation of z ².

Comment ((https://en.wikipedia.org/wiki/Cantelli%27s_inequality): He, Zhang, and Zhang showed :

\Pr(X\geq \lambda )\leq 1-(2{\sqrt {3}}-3){\frac {(1+\lambda ^{2})^{2}}{\mathbb {E} [X^{4}]+6\lambda ^{2}+\lambda ^{4}}}.

In the case $\lambda =0$ this matches a bound in Berger's "The Fourth Moment Method",^]

\Pr(X\geq 0)\geq {\frac {2{\sqrt {3}}-3}{\mathbb {E} [X^{4}]}}.

Definition: if the relative fourth moment of κ = μ₄/σ⁴ than1/κ = σ⁴/μ₄ equal to the peakedness: 1/3 for normal distribution, 5/9 for uniform distribution, and 5/6 for exponential distribution, 1/6 for Laplace distribution (https://en.wikipedia.org/wiki/Laplace_distribution), and (1 - p) / [1- 3p(1-p)] for Bernoulli distribution, (1 - p)/( p² - 9p + 9) geometric distribution (https://testbook. com/question-answer/the-excess-kurtosis-of-the-geometric-distribution--607e64a9c3ce62d9a72ef003), λ ((1+ 3λ ) for a Poisson distribution.

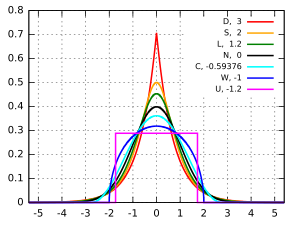
Values of κ - 3, defined as the excess kurtosis:

Probability density functions for selected distributions with mean 0, variance 1 and different excess kurtosis (https://en.wikipedia.org/wiki/Kurtosis)

S: hyperbolic secant distribution, orange curve, excess kurtosis = 2
L: logistic distribution, green curve, excess kurtosis = 1.2
N: normal distribution, black curve (inverted parabola in the log-scale plot), excess kurtosis = 0
C: raised cosine distribution, cyan curve, excess kurtosis = −0.593762...
W: Wigner semicircle distribution, blue curve, excess kurtosis = −1
U: uniform distribution, magenta curve (shown for clarity as a rectangle in both images), excess kurtosis = −1.2.
D: Laplace distribution, also known as the double exponential distribution, red curve (two straight lines in the log-scale plot), excess kurtosis = 3 (c.f. (https://en.wikipedia.org/wiki/Kurtosis)