
- hatékony következtető algoritmusok
- tárgyterületek modellezése (egyetemi, orvosi, műszaki feladatok)
- dialógusokat futtató keretrendszer
- tudásbázisok vizualizációjával.
célvezérelt szabályalapú technikák
adatvezérelt szabályalapú technikák
keretalapú technikák
gépi tanuláson alapuló technikák
induktív technikák
esetalapú technikák.
A szakértői rendszereket gyakran használják az F-mérőszámot olyan területeken, mint a orvosi diagnosztika vagy a csalások felderítése, ahol a "pozitív" esetek (pl. egy betegség jelenléte, csalárd tranzakció) ritkák a "negatív" esetekhez képest. Ilyen esetekben az pontosság (P) metrika 1-hez közeli értéket mutathat akkor is, ha a rendszer minden esetet negatívnak jósol, és a többség valóban negatív. Az F-mérték figyelembe veszi a hamis negatívok és hamis pozitívok arányát is, így valósabb képet ad a rendszer hasznosságáról. Az F-mérték a pontosság (P) és a keresési arány (R) kombinálásával kiegyensúlyozott értékelést nyújt, ami kulcsfontosságú a szakértői rendszerek megbízható teljesítményének mérésére, különösen, ha az adatok nem egyenletesen oszlanak el az osztályok között. F értéke a P és az R harmonikus átlaga*. Ha bármelyik (P vagy R) kicsi → akkor a F érték kicsi lesz, ami nagyon jól illik a bizonytalan döntésekhez a szakértői rendszerekben, ahol nem akarjuk, hogy egy jó mutató „elfedje” a többi rosszat.
A szakértői rendszerek logikai következtetésen és heurisztikákon alapuló módszereket használnak a bizonytalan tudás kezelésére. A szakértői rendszerek a mesterséges intelligencia egyik klasszikus ágát képviselik, szabályalapú logikát használnak, ahol a tényekből és szabályokból vonnak le következtetéseket. A szabályok prioritása határozza meg a végrehajtás sorrendjét. heurisztikák és tapasztalati tudá segítik a döntéshozatalt a bonyolult helyzetekben, mert a szabályok bizonytalan vagy hiányos adatokkal is képesek működni, a bizonytalanság kezelésére más statisztikai és valószínűségszámítási módszereket, például Bayes-hálózatokat vagy a Dempster-Shafer elméletet alkalmazhatnak.

(https://epsombusiness.club/https-invotra-com-ai-business-assistant-for-smes/)
Több szakértő megbízhatósága esetén szakértők hibaarányát vagy tévedési valószínűségét becsüljük: ha a szakértők száma i, és a hibaarány pi , akkor a „várható hibáig eltelt idő” ~ 1/pi Ha átlagos teljesítményt akarunk számítani, akkor a reciprokok számtani átlaga jelenik meg, a harmonikus átlag*, amit döntéselméletben, megbízhatóságelméletben használnak. Ha több alternatív esemény van különböző valószínűségekkel, és ezekből „átlagos” eseménygyakoriságot keresünk, akkor harmonikus átlag az alkalmas. Pl. Markov-láncoknál az átlagos visszatérési időknél, ami egy adott állapot visszatérési idejének valószínűsége. Hasznos, amikor több forrásból érkeznek a valószínűségi becslések, nem szeretnénk, hogy egy „optimista” becslés domináljon. A harmonikus átlag* bünteti a túl kis valószínűségeket, illik a robusztus biztonság a cél, kritikus szemlélethez. A valószínűségek reciprokainak összege tipikusan ott jelenik meg, ahol várakozási idők, ritka események fordulnak elő, sok klasszikus modell mögött ez áll. Pl. a harmonikus közép* több helyen megjelenik, ahol arányok, ráták vagy bizonytalan teljesítmény, találati arány, hibaarány számít, azt szeretnénk, hogy a kis értékek domináljanak (a „szűk keresztmetszet” számít).
Szakértői rendszerekben (pl. orvosi és más diagnózisok) a számtani közép* számítása is gyakori: tömegjelenségek átlagos leírása használjuk számtani középpel* történik. A diagnosztikai folyamat célja általában a legvalószínűbb hiba vagy állapot (hipotézis) beazonosítása a lehető legalacsonyabb költséggel. A hipotéziseket valószínűség/költség sorrendben célszerű vizsgálni.
Soros hipotézis rendszerek, döntések megbízhatóságának számításánál, amikor a rendszer akkor működik, ha minden eleme működik: a legmegbízhatatlanabb elem működési valószínűsége határozza meg az egész rendszer megbízhatóságát. A működési valószínűség reciproka akkor jelenik meg, ha ritka eseményeket, pl. meghibásodásokat várunk, vagy ha a folyamat szekvenciális, amikor a bekövetkezés valószínűségét vizsgáljuk az idő függvényében. Szakértői rendszerekben a harmonikus közepet használják szekvenciális vizsgálatoknál, diagnózisoknál, tesztek egymás utáni alkalmazásánál, hibakeresési fák költségszámításainál.
Szakértői rendszerekben a geometriai közép* (mértani közép) számítását akkor használják, amikor különböző skálájú adatok összevonására, növekedési ráták kezelésére vagy szubjektív ítéletek összesítésére van szükség. Míg a számtani közép* érzékeny a szélsőséges kiugró értékekre, a geometriai közép* kiegyensúlyozottabb eredményt ad, ha az értékek arányokban vagy nagyságrendekben térnek el egymástól, pl. többszempontú döntéstámogatás esetén. A szakértői rendszerek egyik legnépszerűbb algoritmusa az Analitikus Hierarchia Folyamat, ekkor a szakértők páros összehasonlításokat végeznek (pl. mennyivel fontosabb az 'A' szempont a 'B'-nél). Ha több szakértő véleményét kell egyesíteni, a geometriai közép biztosítja, hogy a reciprok vélemények (pl. ha az egyik szakértő szerint kétszer jobb, a másik szerint 1/2-szer) ne oltsák ki egymást, és előnye hogy megőrzi a döntések közötti matematikai konzisztenciát.
A geometriai középértéket számítják, ha a szakértői rendszernek olyan mutatókat kell összegeznie, amelyek mértékegységei és skálái teljesen eltérőek (például egy gép állapotfelmérésénél a hőmérséklet, a rezgés és a zajszint), a számtani átlag félrevezető lehet. Pl. az ENSZ által használt Fejlettségi Index geometriai középpel számol, hogy megakadályozza, hogy egy kiemelkedő részmutató (pl. magas jövedelem) teljesen elfedje egy másik mutató (pl. alacsony oktatási szint) gyengeségét. Geometriai középértéket számítanak ha egy esemény bekövetkezéséhez több, egymástól függő feltétel együttes teljesülése szükséges, és ezeket arányként kezeljük, a geometriai közép* jobban tükrözi a rendszer „átlagos” megbízhatóságát, mint a számtani átlag*.
Informatikai szakértői rendszerekben, ahol különböző algoritmusok sebességét vagy hatékonyságát hasonlítják össze: a geometriai közép az egyetlen olyan átlag, amely független a bázisértéktől. Ha az eredményeket normalizáljuk (egy kiválasztott gép teljesítményéhez viszonyítjuk), a mértani közép* akkor is ugyanazt a sorrendet adja a szoftverek között, bármelyik gépet is választjuk referenciának.
Míg a geometriai középérték nem érzékeny a szélsőséges értékekre, a harmonikus középérték érzékeny a kis értékekre. A számtani közép a nagy kiugró értékekre érzékeny: a statisztikák eredményei függenek a számítás módjától! Minél nagyobb egy valószínűségi változó szórása (varianciája), annál nagyobb lesz a különbség a három átlag között.
A pénzügyi modellekben gyakran használnak log-normális eloszlást. A számtani átlag a portfólió várható értékét mutatja, míg a mértani átlag azt a "tipikus" hozamot, amit egy befektető ténylegesen realizál az idő alatt. A kettő közötti különbséget volatilitási adónak is nevezik. A harmonikus közép a legkonzervatívabb közép. Ha egy rendszerben több párhuzamos folyamat sebességét mérjük, a harmonikus közép adja meg a rendszer tényleges áteresztőképességét, mert a "leglassabb" elem (a legkisebb érték) húzza le leginkább az eredményt.
Valószínűségi eloszlások szempontjából az átlagok viszonya: pl geometriai eloszlásnál az átlagok összehasonlítása. A geometriai eloszlás a diszkrét, „ritka esemény bekövetkezéséig tartó várakozást” modellezi. A geometriai eloszlás esetén a három átlag közötti különbség a kockázatot és az aszimmetriát mutatja: amikor egy folyamat "megbízhatóságát" akarjuk mérni, a számtani közép a legrosszabb mutató, mert túl optimistának tűnhet a nagy kilengések miatt. A harmonikus közép használata akkor indokolt, ha a "leggyorsabb" eredmények dominanciáját akarjuk látni, vagy ha rátákkal (pl. egységnyi idő alatti sikerek száma) dolgozunk.
Érdekesség: ha az intervallum alját közelítjük a nullához, a harmonikus közép nullához tart, a mértani közép is csökken, de a számtani közép stabilan a felezőponton marad, ezért nem használhatunk harmonikus közepet olyan adatsoroknál, ahol előfordulhat nulla közeli érték.
Minden tudományág (pl. fizika, közgazdaságtan) azt a középértéket választja, amelyik megőrzi a vizsgált rendszer fizikai (pénzügyi) állandóját. Fizikában a megtette távolság, a munka, az energia..megmaradási törvények. Fizikában és a mérnöki tudományokban a számtani közép mellett a harmonikus középet is használjuk, pl. fizikában az átlagolás gyakran arányokra, rátákra (időegység alatti teljesítményre) vonatkozik, amikor a harmonikus közép jellemző. Pl. sebességeknél a lassú szakaszhoz több idő szükséges, az nagyobb súllyal számít az időalapú átlagban. A párhuzamosan kapcsolt ellenállások eredője a harmonikus közép elvén alapul. A fizikai rendszerekben gyakran a "leggyengébb láncszem" vagy a lassú folyamat határozza meg az összteljesítményt.
A hétköznapi életben (pl. diétázás) melyik átlaggal szoktuk a legtöbb hibát elkövetni? A diétázás és a fogyás világában a legtöbb hibát azért követjük el, mert számtani fejjel gondolkodunk ott, ahol harmonikus vagy mértani folyamatok zajlanak. A testünk ugyanis nem egy egyszerű gép, hanem egy biológiai rendszer. A két leggyakoribb "átlagolási csapda" a diétában: az "átlagos kalóriadeficit" csapdája (számtani vs. harmonikus közép). Sokan úgy számolnak: "Hétfőtől szombatig tartom a napi 1500 kalóriát, vasárnap pedig tartok egy 'csalónapot' 4500 kalóriával. Az átlagom így napi ~1900, ami még belefér!" De a szervezetünk anyagcseréje nem számtani átlaggal működik. A hirtelen, hatalmas kalóriatöbblet (inzulin-tüske, raktározási hormonok) nagyobb rombolást végez, mint amit a hatnapos fegyelem számtani javulása mutat. Egy diéta sikere inkább a harmonikus középpel írható le: a "leggyengébb láncszem" (a legrosszabb napod) sokkal súlyosabban rontja az eredményt, mint ahogy azt a számtani közép mutatja. A súlyvesztés üteme (mértani szemlélet): a fogyást gyakran fix kilókban mérjük (pl. "heti 1 kg"), ami számtani megközelítés, de a testtömeg-változás valójában egy százalékos folyamat. Ezért aki 100 kg-ról indul, annak az 1 kg fogyás a testtömege 1%-a, de aki 70 kg-ról, annak az 1 kg már 1,4%-os drasztikus csökkenés. A profi sportolóknál a dietetikusok mértani középpel mérik a fogyást, nem a leadott kilók száma a fontos, hanem a testsúlyhoz viszonyított arány. Véralkohol színtnél, gyógyszerek adagolásánál is a testsúlyra vonatkoztatják a mennyiségeket. A diétában a harmonikus középet használják: egyetlen hiba (vagy egy tartós mikro-tápanyag hiánya) képes nullázni az összes többi erőfeszítést, függetlenül attól, hogy a többi nap "átlagosan" helyes étkezésétől.
A négyzetes közép* gyakran használt statisztikai mérőszám a matematikában és a fizikában, különösen a változó, ingadozó értékek jellemzésére, a szakértői rendszerek döntéshozatalnál, vagy bizonytalan helyzetek kezelésében ritkán alkalmazzák. Fő alkalmazási területei a szakértői rendszereken kívül vannak, a fizikai és mérnöki tudományok területén. A négyzetes középérték (RMS, Root Mean Square) a váltakozó áram vagy feszültség effektív értékének kiszámítására szolgál például, ami azt az egyenáramú egyenértéket jelenti, amely ugyanazt az energiaveszteséget okoz. Statisztikában a fontos szóródási mérőszám (a szórás) mérőszámaként jelenik meg.
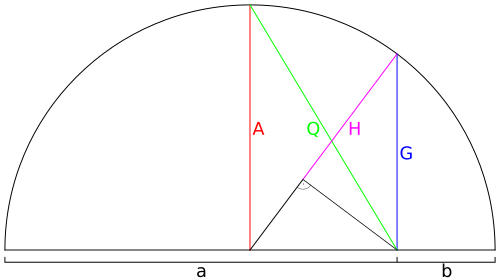
Várható érték, számtani közép (A): a várható érték becslése a számtani közép, azaz a tényezők, azaz a valószínűségi változók összege osztva a tényezők számával. A valószínűségszámításban a véletlen jelenségek átlagos eredményét írja le. A tényezők valószínűségeivel súlyozott összeggel egyenlő. A számtani középben a két adatsor közül nagyobb súlyt kapnak a kisebb adatok; a harmonikus közép minden adatot ugyanolyan súllyal tekint.
Kvartilisek (a sokaságot négy részre osztják),
Kvintilisek (a sokaságot öt részre osztják),
Decilisek (a sokaságot tíz részre osztják),
Percentilisek (a sokaságot száz részre osztják).
